题目内容
19.函数f(x)=(a-1)ln x+$\frac{a}{x}$+bx+2(a,b∈R).(1)若函数f(x)的图象在点(1,f(1))处的切线方程为x-y+1=0,求实数a,b的值;
(2)已知b=1,当x>1时,f(x)>0,求实数a的取值范围.
分析 (1)由题知得f(1)=b+a+2=2,f′(1)=b-1=1,解得a=-2,b=2;
(2)当b=1时,f(x)=(a-1)lnx+$\frac{a}{x}$+x+2,
f′(x)=$\frac{a-1}{x}-\frac{a}{{x}^{2}}$+1=$\frac{(x-1)(x+a)}{{x}^{2}}$
分以下两种情况讨论:当a≥-1,当a<-1,求出最小值,只需f(x)min>0即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),f′(x)=$\frac{a-1}{x}-\frac{a}{{x}^{2}}$+b.
由题知得f(1)=b+a+2=2,f′(1)=b-1=1,解得a=-2,b=2…(5分)
(2)当b=1时,f(x)=(a-1)lnx+$\frac{a}{x}$+x+2,
∴f′(x)=$\frac{a-1}{x}-\frac{a}{{x}^{2}}$+1=$\frac{(x-1)(x+a)}{{x}^{2}}$…(7分)
当a≥-1时,-a≤1,当x>1时,f′(x)>0,∴f(x)在(1,+∞)上是增函数,
∴当x>1时,f(x)>f(1)=a+3≥2,∴a≥-1满足题意…(9分)
当a<-1时,-a>1,当1<x<-a时,f′(x)<0,当x>-a时,f′(x)>0,
∴f(x)在区间(1,-a)上是减函数,在区间(-a,+∞)是增函数,
∴f(x)min=f(-a)=(a-1)ln(-a)+$\frac{a}{-a}$-a+2=(a-1)ln(-a)-a+1,
由题知f(x)min=(a-1)ln(-a)-a+1>0,解得a>-e,
∴-e<a<-1…(11分)
综上所述,实数a的取值范围为(-e,+∞).(12分)
点评 本题考查了导数的几何意义,利用导数求函数的最值,考查了分类讨论思想,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 都小于2 | B. | 都大于2 | ||
| C. | 至少有一个不大于2 | D. | 至少有一个不小于2 |
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=∅ |
| A. | (-∞,2) | B. | (-∞,3] | C. | [0,2) | D. | [0,3] |
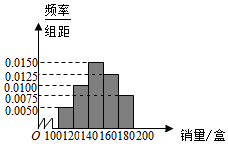 某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.