题目内容
7.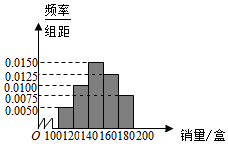 某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.(Ⅰ)根据直方图估计这个开学季内市场需求量x的平均数和众数;
(Ⅱ)将y表示为x的函数;
(Ⅲ)根据频率分布直方图估计利润y不少于1350元的概率.
分析 (Ⅰ)由频率分布直方图能估计这个开学季内市场需求量x的平均数和众数.
(Ⅱ)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,当100<x≤200时,y=10x-5(150-x)=15x-750,当150<x≤200时,y=10×150=1500,由此能将y表示为x的函数.
(Ⅲ)由利润不少于1350元,得150x-750≥750,由此能求出利润不少于1350元的概率.
解答 解:(Ⅰ)由频率分布直方图得:最大需求量为150盒的频率为0.015×20=0.3.
这个开学季内市场需求量的众数估计值是150.
需求量为[100,120)的频率为0.005×20=0.1,
需求量为[120,140)的频率为0.01×20=0.2,
需求量为[140,160)的频率为0.015×20=0.3,
需求量为[160,180)的频率为0.0125×20=0.25,
需求量为[180,200)的频率为0.0075×20=0.15,
则平均数:$\overline{x}$=110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153.
(Ⅱ)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,
所以当100<x≤200时,y=10x-5(150-x)=15x-750,
当150<x≤200时,y=10×150=1500,
所以y=$\left\{\begin{array}{l}{15x-750,100≤x≤150}\\{1500,150<x≤200}\end{array}\right.$,x∈N.
(Ⅲ)因为利润不少于1350元,
所以150x-750≥750,解得x≥140.
所以由(Ⅰ)知利润不少于1350元的概率p=1-0.1-0.2=0.7.
点评 本题考查平均数、函数表达式、概率的求法,考查频率分布直方图的应用,考查运算求解能力,考查函数与方程思想、数形结合思想,是基础题.

| A. | -1 | B. | 1 | C. | -i | D. | i |
| A. | k=-1 | B. | k<-1 | C. | -1≤k≤1 | D. | k≤-1 |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
| A. | 3,11,19,27,35 | B. | 5,15,25,35,46 | C. | 2,12,22,32,42 | D. | 4,11,18,25,32 |
