题目内容
求不等式3≤|x2-1|<4的解集.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:把要解的不等式等价转化为与之等价的两个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答:
解:由不等式3≤|x2-1|<4 可得
,即
,即
,
故不等式的解集为{x|-
<x≤-2,或 2≤x<
}.
|
|
|
故不等式的解集为{x|-
| 5 |
| 5 |
点评:本题主要考查绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若α=β,则sinα=sinβ”的逆命题为真命题 | ||
| B、已知命题p:函数f(x)=tanx的定义域为{x|x≠kπ,k∈Z},命题q:?x∈R,x2-x+1≥0;则命题p∧q为真命题 | ||
C、“a=2”是“直线y=-ax+2与直线y=
| ||
| D、命题“?x∈R,使得x2+2x+3<0”的否定形式是真命题 |
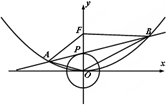 已知点F(0,2)是抛物线x2=ay的焦点.
已知点F(0,2)是抛物线x2=ay的焦点.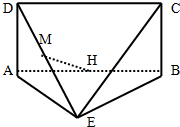 已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为
已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为