题目内容
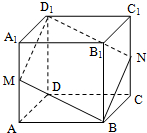 在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:
在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:①四边形BMD1N一定是平行四边形;
②四边形BMD1N有可能是正方形;
③四边形BMD1N 在底面ABCD内的投影一定是正方形;
④平面BMD1N 有可能垂直于平面BB1D1D.
其中正确的有
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:根据面面平行和正方体的几何特征进行判断,利用一些特殊情况进行说明.
解答:
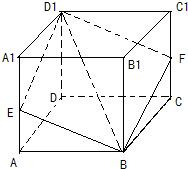 解:如图:
解:如图:
①由平面BCB1C1∥平面ADA1D1,并且B、E、F、D1四点共面,
∴ED1∥BF,同理可证,FD1∥EB,故四边形BFD1E一定是平行四边形,故①正确;
②若BFD1E是正方形,有ED1⊥BE,这个与A1D1⊥BE矛盾,故②错误;
③由图得,BFD1E在底面ABCD内的投影一定是正方形ABCD,故③正确;
④当点E和F分别是对应边的中点时,平面BFD1E⊥平面BB1D1,故④正确.
故答案为:①③④.
 解:如图:
解:如图:①由平面BCB1C1∥平面ADA1D1,并且B、E、F、D1四点共面,
∴ED1∥BF,同理可证,FD1∥EB,故四边形BFD1E一定是平行四边形,故①正确;
②若BFD1E是正方形,有ED1⊥BE,这个与A1D1⊥BE矛盾,故②错误;
③由图得,BFD1E在底面ABCD内的投影一定是正方形ABCD,故③正确;
④当点E和F分别是对应边的中点时,平面BFD1E⊥平面BB1D1,故④正确.
故答案为:①③④.
点评:本题主要考查了正方体的几何特征,利用面面平行和线线垂直,以及特殊情况进行判断,考查了空间信息能力和逻辑思维能力.

练习册系列答案
相关题目
设集合S={x|x>-2},T={x|-4≤x≤1},则(∁RS)∪T=( )
| A、(-2,1] |
| B、(-∞,-4] |
| C、(-∞,1] |
| D、[1,+∞) |
设两非零向量
=(x1,y1),
=(x2,y2),下列叙述错误的是( )
| a |
| b |
A、若
| ||||||||
B、若
| ||||||||
C、若
| ||||||||
D、若
|
已知异面直线a、b所成角为
,经过定点P与a、b所成的角均为
的平面有( )
| π |
| 3 |
| π |
| 6 |
| A、1个 | B、2个 | C、3个 | D、无数 |
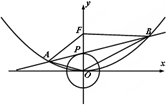 已知点F(0,2)是抛物线x2=ay的焦点.
已知点F(0,2)是抛物线x2=ay的焦点.