Question

己知函数f（x）=|1-

1

x

|，（x＞0），
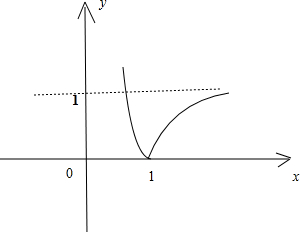
（1）画出函数的草图；
（2）当0＜a＜b，且f（a）=f（b）时，求

1

a

+

1

b

的值；
（3）若存在实数a，b（0＜a＜b），使得函数y=f（x）的定义域为[a，b]时，值域[ma，mb]，其中m≠0，求实数m的取值范围．

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：（1）f（x）=|1-

1

x

|，可看做先由函数y=

-1

x

向上平移1个单位，再把x轴以下的部分翻到x轴以上；
（2）当0＜a＜b，且f（a）=f（b）时，可得a＜1，b＞1，故f(a)=

1

a

-1，f(b)=

-1

b

+1，由f（a）=f（b），得

1

a

-1=

-1

b

+1，且

1

a

+

1

b

=2．
（3）f分三种情况：
①当a、b∈（0，1]、②当a∈（0，1]，b∈（1，+∞）、③当a、b∈[1，+∞）时，讨论函数的单调性，得方程解决．

解答： 解：（1）f（x）=|1-

1

x

|，可看做先由函数y=

-1

x

向上平移1个单位，再把x轴以下的部分翻到x轴以上，图象如图：

（2）当0＜a＜b，且f（a）=f（b）时，可得a＜1，b＞1
∴f(a)=

1

a

-1，f(b)=

-1

b

+1
∵f（a）=f（b），∴

1

a

-1=

-1

b

+1，∴

1

a

+

1

b

=2．
（3）易知m＞0
f分三种情况：
①当a、b∈（0，1]时，因为f（x）递减，∴

f(a)=mb f(b)=ma

，∴

1 a -1=mb 1 b -1=ma

，∴

1-a=mab 1-b=mab

，
∴1-a=1-b，∴a=b与已知矛盾；
②当a∈（0，1]，b∈（1，+∞）时，显然1∈[a，b]，而f（1）=0，
∴0∈[ma，mb]，而ma＞0，矛盾；
③当a、b∈[1，+∞）时，因为f（x）递增，∴

f(a)=ma f(b)=mb

，即

-1 a +1=ma -1 b +1=mb

，
∴

ma2-a+1=0 mb2-b+1=0

，∴a与b为方程mx²-x+1=0的两根，
∵a、b都大于1，∴方程mx²-x+1=0有两个大于1的不等根，
∴

△=1-4m＞0 - -1 2m ＞1 m-1+1＞0

，解得0＜m＜

1

4

，
∴实数m的取值范围为{m|0＜m＜

1

4

}．

点评：本题考查函数的值域，涉及函数的单调性和运用一元二次方程探讨问题，属中档题．