题目内容
5.已知△ABC中,$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{a+b-c}$=c且acosB=bcosA,试判断△ABC的形状.(等边三角形)分析 acosB=bcosA,利用余弦定理可得a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=b$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,化为:a=b.代入$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{a+b-c}$=c,可得:a=c,即可得出.
解答 解:∵acosB=bcosA,∴a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=b$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,化为:a=b.
又$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{a+b-c}$=c,∴2a2-c2=c(2a-c),化为:a=c,
∴a=b=c,
∴△ABC为等边三角形.
点评 本题考查了余弦定理、三角形形状的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知直线l1:A1x+B1y+1=0,直线l2:A2x+B2y+1=0,A1,A2,B1,B2∈R,则“l1⊥l2”的充分且必要条件是( )
| A. | A1A2-B1B2=0 | B. | A1A2+B1B2=0 | C. | A1B2-A2B1=0 | D. | A1B2+A2B1=0 |
10.甲、乙、丙3名教师安排在10月1日至5日的5天中值班,要求每人值班一天且每天至多安排一人.其中甲不在10月1日值班且丙不在10月5日值班,则不同的安排方法有( )种.
| A. | 36 | B. | 39 | C. | 42 | D. | 45 |
17.设集合A={4,5,6,9},B={3,4,6,8,9},全集U=A∪B,则集合∁U(A∩B)的元素个数共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
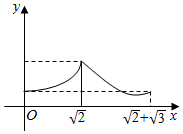
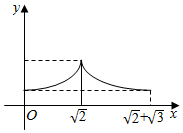
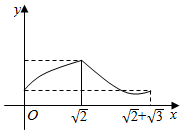
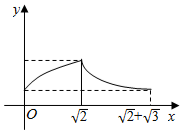
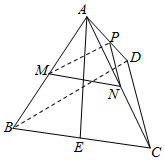 如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )
如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )