题目内容
16．已知直线l1：A1x+B1y+1=0，直线l2：A2x+B2y+1=0，A1，A2，B1，B2∈R，则“l1⊥l2”的充分且必要条件是（ ）| A． | A1A2-B1B2=0 | B． | A1A2+B1B2=0 | C． | A1B2-A2B1=0 | D． | A1B2+A2B1=0 |
分析 结合直线垂直的等价条件，利用充分条件和必要条件的定义进行判断．
解答 解：两条直线A1x+B1y+1=0，A2x+B2y+1=0互相垂直?A1A2+B1B2=0，
故两条直线A1x+B1y+1=0，A2x+B2y+1=0互相垂直的充分必要条件是A1A2+B1B2=0，
故选：B．
点评 本题主要考查充分条件和必要条件的判断，利用直线垂直的条件是解决本题的关键．
练习册系列答案
相关题目
目前很多朋友都加入了微信群，大多数群成员认为有思想的群不仅仅是群里的人转发与主题有关的网页文章，而且群成员这间还有文字或语音的交流，因此规定$\frac{网页类型分享}{文字语音聊天}$为“群健康度”，为此群主统计了一年的群里的聊天记录（假定该群由群主同意邀请，也无插入广告），并将聊天记录中的网页类型分享和文字语音聊天内容进行了分类统计，并按照“群健康度”制作了分析趋势图如图，假定“群健康度”小于20%为群氛围优良，“群健康度”大于30%为群氛围不合理．
4．已知向量$\overrightarrow{a}$=（4，2），$\overrightarrow{b}$=（x，3），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则x的值是（ ）
| A． | -6 | B． | 6 | C． | -$\frac{3}{2}$ | D． | $\frac{3}{2}$ |
11．
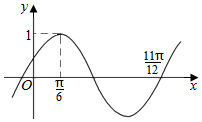函数$f（x）=Asin（ωx+φ）\;（A＞0\;，\;ω＞0\;，\;|φ|＜\frac{π}{2}）$的部分图象如图所示，则将y=f（x）的图象向右平移$\frac{π}{6}$个单位后，得到的函数图象的解析式为（ ）
函数$f（x）=Asin（ωx+φ）\;（A＞0\;，\;ω＞0\;，\;|φ|＜\frac{π}{2}）$的部分图象如图所示，则将y=f（x）的图象向右平移$\frac{π}{6}$个单位后，得到的函数图象的解析式为（ ）| A． | y=sin2x | B． | $y=sin（2x+\frac{2π}{3}）$ | C． | $y=sin（2x-\frac{π}{6}）$ | D． | y=cos2x |
1．在△ABC中，D为线段BC上一点，且$BD=\frac{1}{5}BC$，以向量$\overrightarrow{AB}，\overrightarrow{AC}$作为一组基底，则$\overrightarrow{AD}$等于（ ）
| A． | $\frac{1}{5}\overrightarrow{AB}+\frac{4}{5}\overrightarrow{AC}$ | B． | $\frac{2}{5}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}$ | C． | $\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}$ | D． | $\frac{4}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$ |