题目内容
20.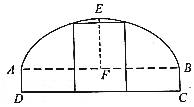 如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.
如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.
分析 建立如图所示的坐标系,求出抛物线的方程,即可求出求出能使载重卡车通过隧道时t的最小整数值.
解答 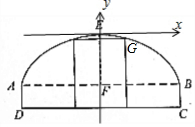 解:建立如图所示的坐标系,则B($\frac{t}{2}$,-$\frac{t}{4}$),
解:建立如图所示的坐标系,则B($\frac{t}{2}$,-$\frac{t}{4}$),
设抛物线方程为x2=ay,则$\frac{{t}^{2}}{4}=a•(-\frac{t}{4})$,∴a=-t,
∴x2=-ty,
由题意,x=1.1,y=-$\frac{1.21}{t}$
∴-$\frac{1.21}{t}$+$\frac{t}{4}$≥2,
t=8,-$\frac{1.21}{t}$+$\frac{t}{4}$<2,t=9,-$\frac{1.21}{t}$+$\frac{t}{4}$>2,
∴能使载重卡车通过隧道时t的最小整数值等于9.
故答案为9.
点评 本题考查抛物线的应用,考查学生的计算能力,确定抛物线的方程是关键.

练习册系列答案
相关题目
10.已知复数z满足(z-1)i=|i+1|,则z=( )
| A. | -2-i | B. | 2-i | C. | $1-\sqrt{2}i$ | D. | $-1-\sqrt{2}i$ |
12.已知$\frac{1-i}{z}$=(1+i)2(i为虚数单位),则复数z的共轭复数为( )
| A. | -$\frac{1}{2}$-$\frac{1}{2}$i | B. | -$\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
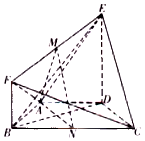 在如图所示的几何体ABCDEF中,四边形ABCD是等腰梯形,AD∥BC,∠ABC=60°,AB=$\frac{1}{2}$BC=1,DE⊥平面ABCD,BF∥DE,DE=2BF,M,N分别是EF、BC的中点.
在如图所示的几何体ABCDEF中,四边形ABCD是等腰梯形,AD∥BC,∠ABC=60°,AB=$\frac{1}{2}$BC=1,DE⊥平面ABCD,BF∥DE,DE=2BF,M,N分别是EF、BC的中点.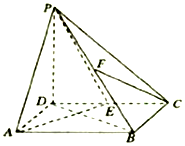 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.