题目内容
9.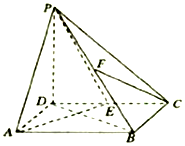 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别是CD,PB的中点.求证:(Ⅰ)CF∥平面PAE;
(Ⅱ)平面PAE⊥平面PBD.
分析 (Ⅰ)根据线面平行的判定定理即可证明CF∥平面PAE;
(Ⅱ)根据线面垂直的判定定理证明AE⊥平面PBD,即可证明平面PAE⊥平面PBD.
解答  证明:(Ⅰ)取AB的中点N,连接FN,EN,
证明:(Ⅰ)取AB的中点N,连接FN,EN,
在△PAB中,FN为中位线,
∴FN∥AB,FN=$\frac{1}{2}$AB,
∵CE=$\frac{1}{2}$AB,CE∥AB,
∴CE∥FN,CE=FN,
∴四边形CENF为平行四边形,
∴CF∥EN,
∵EN?面PAE,CF?面PAE,
∴CF∥平面PAE;
(Ⅱ)∵PD⊥平面ABCD,AE?平面ABCD,
∴PD⊥AE.
设AE∩BD=M,∵E为CD的中点,
∴$\frac{DE}{AB}=\frac{DM}{BM}=\frac{EM}{AM}=\frac{1}{2}$,
则△DME∽△AMB,
在矩形ABCD中,AE=$\sqrt{3}$,BD=$\sqrt{6}$,
∴DM2+EM2=$\frac{1}{3}+\frac{2}{3}=1$=DE2,
即△DME为直角三角形,即AE⊥BD,
∵PD∩BD=D,PD?面PBD,BD?面PBD,
∴AE⊥平面PBD,
∵AE?平面PAE,
∴平面PAE⊥平面PBD.
点评 本题主要考查空间线面平行和线面垂直、面面垂直的判定,根据相应的判定定理是解决本题的关键.

练习册系列答案
相关题目
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1和F2,以F1F2为直径的圆与双曲线的一个交点为P,若|PF1|=a,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
14.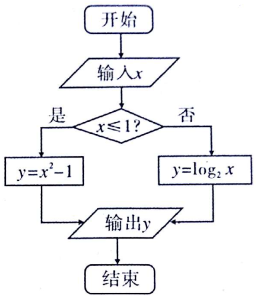 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )| A. | [0,2] | B. | [-1,2] | C. | [-1,15] | D. | [2,15] |
11.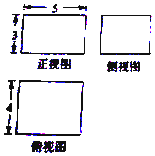 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
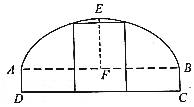 如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.
如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.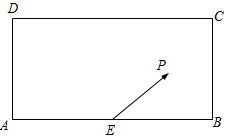 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.