题目内容
10.已知复数z满足(z-1)i=|i+1|,则z=( )| A. | -2-i | B. | 2-i | C. | $1-\sqrt{2}i$ | D. | $-1-\sqrt{2}i$ |
分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:复数z满足(z-1)i=|i+1|,则-i•(z-1)i=-i•|i+1|,则z-1=-$\sqrt{2}$i,
∴z=1-$\sqrt{2}$i,
故选:C.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.已知函数$f(x)=\left\{\begin{array}{l}x+1,0≤x≤1\\ \frac{1}{2}sin({\frac{π}{4}x})+\frac{3}{2},1<x≤4\end{array}\right.$,若不等式f2(x)-af(x)+2<0在x∈[0,4]上恒成立,则实数a取值范围是( )
| A. | $a>2\sqrt{2}$ | B. | $2\sqrt{2}<a<3$ | C. | a>3 | D. | $3<a<2\sqrt{3}$ |
2.已知双曲线C:$\frac{x^2}{{a{\;}^2}}-\frac{y^2}{{b{\;}^2}}$=1的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某一条渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$且$\overrightarrow{OQ}=5\overrightarrow{OP}$,则双曲线C的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
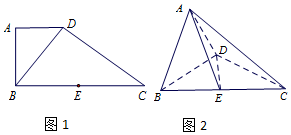 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体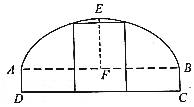 如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.
如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.