题目内容
12.已知$\frac{1-i}{z}$=(1+i)2(i为虚数单位),则复数z的共轭复数为( )| A. | -$\frac{1}{2}$-$\frac{1}{2}$i | B. | -$\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
分析 把已知等式变形,然后利用复数代数形式的乘除运算化简,则答案可求.
解答 解:由$\frac{1-i}{z}$=(1+i)2,得$z=\frac{1-i}{(1+i)^{2}}=\frac{1-i}{2i}=\frac{(1-i)i}{2{i}^{2}}=\frac{1+i}{-2}=-\frac{1}{2}-\frac{1}{2}i$.
∴$\overline{z}=-\frac{1}{2}+\frac{1}{2}i$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础的计算题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
2.已知双曲线C:$\frac{x^2}{{a{\;}^2}}-\frac{y^2}{{b{\;}^2}}$=1的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某一条渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$且$\overrightarrow{OQ}=5\overrightarrow{OP}$,则双曲线C的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
3.某供货商计划将某种大型节日商品分别配送到甲、乙两地销售.据以往数据统计,甲、乙两地该商品需求量的频率分布如下:
甲地需求量频率分布表示:
乙地需求量频率分布表:
以两地需求量的频率估计需求量的概率
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
甲地需求量频率分布表示:
| 需求量 | 4 | 5 | 6 |
| 频率 | 0.5 | 0.3 | 0.2 |
| 需求量 | 3 | 4 | 5 |
| 频率 | 0.6 | 0.3 | 0.1 |
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1和F2,以F1F2为直径的圆与双曲线的一个交点为P,若|PF1|=a,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
14.已知O是△ABC的外心,∠C=45°,若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$(m,n∈R),则m+n的取值范围是( )
| A. | [$-\sqrt{2}$,$\sqrt{2}$] | B. | [$-\sqrt{2}$,1) | C. | [$-\sqrt{2}$,-1) | D. | (1,$\sqrt{2}$] |
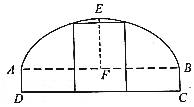 如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.
如图所示,一辆装载集装箱的载重卡车高为3米,宽为2.2米,欲通过断面上部为抛物线形,下部为矩形ABCD的隧道.已知拱口宽AB等于拱高EF的4倍,AD=1米.若设拱口宽度为t米,则能使载重卡车通过隧道时t的最小整数值等于9.