题目内容
函数f（x）=lnx+x3-9的零点所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
考点：函数零点的判定定理,二分法求方程的近似解
专题：函数的性质及应用
分析：根据函数f（x）在（0，+∞）上是增函数，f（2）＜0，f（3）＞0，可得函数f（x）在区间（2，3）上有唯一的零点．
解答：
解：由于函数f（x）=lnx+x3-9在（0，+∞）上是增函数，
f（2）=ln2-1＜0，f（3）=ln3＞0，故函数f（x）=lnx+x3-9在区间（2，3）上有唯一的零点，
故选：C．
f（2）=ln2-1＜0，f（3）=ln3＞0，故函数f（x）=lnx+x3-9在区间（2，3）上有唯一的零点，
故选：C．
点评：本题主要考查函数的单调性，函数零点的判定定理，属于基础题．
练习册系列答案
字词句段篇系列答案
相关题目
如图所示的三视图的几何体的体积为（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
在跳水比赛中，七位裁判为一选手打出的分数如下：9.0，8.9，9.0，9.5，9.3，9.4，9.3，去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为（ ）
| A、9.2，0.02 |
| B、9.2，0.028 |
| C、9.3，0.02 |
| D、9.3，0.028 |
确定结论“X与Y有关系”的可信度为99.5%时，则随即变量k2的观测值k必须（ ）
| A、小于7.879 |
| B、大于10.828 |
| C、小于6.635 |
| D、大于2.706 |
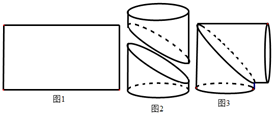工人师傅在如图1的一块矩形铁皮上画一条曲线，沿曲线剪开，将所得到的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．工人师傅所画的曲线是（ ）| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
在△ABC中，A，B，C所对的边分别是a，b，c，满足3a2+3b2=c2+4ab，现设f（x）=tanx，则（ ）
| A、f（sinA）≤f（cosB） |
| B、f（sinA）≥f（cosB） |
| C、f（sinA）≤f（sinB） |
| D、f（cosA）≤f（cosB） |