题目内容
已知数列{an},Sn为其前n项和,且Sn+1=4an+2.(n∈N*),a1=1,
(1)设bn=an+1-2an,求bn
(2)设cn=
,求证:{cn}是等差数列
(3)求an.
(1)设bn=an+1-2an,求bn
(2)设cn=
| an |
| 2n |
(3)求an.
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:(1)在数列递推式中取n=n-1得另一递推式,作差后即可得到数列{bn}是以3为首项,以2为公比的等比数列,由等比数列的通项公式得答案;
(2)由bn=an+1-2an=3•2n-1,两边同时除以2n+1即可证得cn=
为等差数列;
(3)由等差数列的通项公式求得cn,即可得到an.
(2)由bn=an+1-2an=3•2n-1,两边同时除以2n+1即可证得cn=
| an |
| 2n |
(3)由等差数列的通项公式求得cn,即可得到an.
解答:
解:(1)由Sn+1=4an+2,得
Sn=4an-1+2(n≥2),
两式作差得:an+1=4an-4an-1(n≥2),
即an+1-2an=2(an-2an-1)(n≥2),
∴bn=2bn-1(n≥2).
由Sn+1=4an+2,a1=1,求得a2=5.
∴a2-2a1=5-2=3,即b1=3.
∴数列{bn}是以3为首项,以2为公比的等比数列,
则bn=3•2n-1;
(2)由bn=an+1-2an=3•2n-1,得
-
=
,
又
=
,
∴数列{
}构成以
为首项,以
为公差的等差数列,
∵cn=
,
∴{cn}是以
为首项,以
为公差的等差数列;
(3)由(2)知,
=
+
(n-1)=
n-
,
∴an=
(3n-1)•2n.
Sn=4an-1+2(n≥2),
两式作差得:an+1=4an-4an-1(n≥2),
即an+1-2an=2(an-2an-1)(n≥2),
∴bn=2bn-1(n≥2).
由Sn+1=4an+2,a1=1,求得a2=5.
∴a2-2a1=5-2=3,即b1=3.
∴数列{bn}是以3为首项,以2为公比的等比数列,
则bn=3•2n-1;
(2)由bn=an+1-2an=3•2n-1,得
| an+1 |
| 2n+1 |
| an |
| 2n |
| 3 |
| 4 |
又
| a1 |
| 2 |
| 1 |
| 2 |
∴数列{
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
∵cn=
| an |
| 2n |
∴{cn}是以
| 1 |
| 2 |
| 3 |
| 4 |
(3)由(2)知,
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
∴an=
| 1 |
| 4 |
点评:本题考查了数列递推式,考查了等比关系与对称关系的确定,考查了等差数列的通项公式,是中档题.

练习册系列答案
相关题目
对于定义域为R的奇函数f(x),下列结论成立的是( )
| A、f(x)-f(-x)>0 |
| B、f(x)-f(-x)≤0 |
| C、f(x)•f(-x)≤0 |
| D、f(x)•f(-x)>0 |
 在空间四边形ABCD中,G为△BCD的重心,E,F分别为边CD和AD的中点,试化简
在空间四边形ABCD中,G为△BCD的重心,E,F分别为边CD和AD的中点,试化简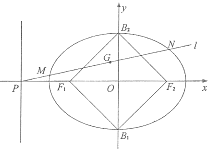 如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ).
如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ). 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=