题目内容

函数y=3sin（2x+
π
4
）的图象如何由函数y=sinx的图象变换得到？
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件利用函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答： 解：把函数y=sinx的图象向左平移
π
4
个单位，可得函数y=sin（x+
π
4
）的图象，
再把所得图象上的各点的横坐标变为原来的
1
2
倍，即可得到函数y=sin（2x+
π
4
）的图象；
再把所得图象上的各点的纵坐标变为原来的3倍，即可得到函数y=3sin（2x+
π
4
）的图象．
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
某房地产开发商投资81万元建一座写字楼，第一年装修费为1万元，以后每年增加2万元，把写字楼出租，每年收入租金30万元．
（Ⅰ）若扣除投资和各种维修费，则从第几年开始获取纯利润？
（Ⅱ）若干年后开发商为了投资其他项目，有两种处理方案：
①年平均利润最大时以46万元出售该楼；　
②纯利润总和最大时，以10万元出售该楼，
问哪种方案盈利更多？
解方程：2（lgx）2-lgx4+1=0．
已知tanα=-
15
，且α∈（
3π
2
，2π），则cosα=
 
．
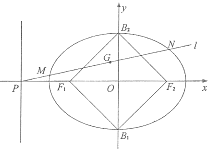如图，已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形（记为Q ）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点P是椭圆C的左准线与x轴的交点，过点P的直线l与椭圆C相交于M，N两点、．当线段MN的中点G落在正方形Q内（包括边界）时，求直线L的斜率的取值范围．
给出下列命题：
①已知集合M满足∅?M⊆{1，2，3}，且M中至少有一个奇数，这样的集合M有6个；
②已知函数f（x）=
33x-1
ax2+ax-3
的定义域是R，则实数a的取值范围是（-12，0）；
③函数f（x）=loga（x-3）+1（a＞0且a≠1）图象恒过定点（4，2）；
④已知函数f（x）=x2+bx+c对任意实数t都有f（3+t）=f（3-t），则f（1）＞f（4）＞f（3）．
其中正确的命题序号是
 
（写出所有正确命题的序号）
如图，四棱锥P-ABCD中，底面ABCD为是矩形，PA⊥底面ABCD，E为棱PD的中点，AP=2，AD=2
3
，且三棱锥E-ACD的体积为
3
．
（Ⅰ）求证：PB∥平面AEC；
（Ⅱ）求直线AE与平面PAC所成角的正弦值．
求下列函数的定义域：
（1）y=
1
1-log7x

（2）y=
log
1
2
x

（3）y=
(
1
5
)x-1

（4）y=log2（x2+x-2）
（5）y=
log0.1(3x-2)

（6）y=
lg(2x-1)
1-x2
．
已知等轴双曲线经过点(2
3
，-4)，则双曲线的实轴长为（　　）
A、4
B、8
C、6
D、4
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网