题目内容
已知两点A(-2,-3),B(3,0)关于直线l对称,
(Ⅰ)求直线l方程;
(Ⅱ)求直线l在x轴上的截距.
(Ⅰ)求直线l方程;
(Ⅱ)求直线l在x轴上的截距.
考点:直线的一般式方程,直线的点斜式方程
专题:直线与圆
分析:(Ⅰ)由题意可知l⊥AB,且线段AB的中点C(
,-
)在直线l上.由垂直关系可得斜率,可得直线的点斜式方程,化为一般式即可;(Ⅱ)在直线l方程中令y=0可解得x值即为所求.
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(Ⅰ)由题意可知l⊥AB,且线段AB的中点C(
,-
)在直线l上.
又线段AB的斜率为kAB=
=
,
由垂直关系可得直线l的斜率为-
,
再由线段AB的中点在直线l上可得y+
=-
(x-
)
化为一般式可得5x+3y+2=0
(Ⅱ)在直线l方程5x+3y+2=0中令y=0可解得x=-
,
∴直线l在轴上的截距为-
| 1 |
| 2 |
| 3 |
| 2 |
又线段AB的斜率为kAB=
| -3-0 |
| -2-3 |
| 3 |
| 5 |
由垂直关系可得直线l的斜率为-
| 5 |
| 3 |
再由线段AB的中点在直线l上可得y+
| 3 |
| 2 |
| 5 |
| 3 |
| 1 |
| 2 |
化为一般式可得5x+3y+2=0
(Ⅱ)在直线l方程5x+3y+2=0中令y=0可解得x=-
| 2 |
| 5 |
∴直线l在轴上的截距为-
| 2 |
| 5 |
点评:本题考查直线的一般式方程和直线的截距,属基础题.

练习册系列答案
相关题目
设曲线y=
与x轴所围成的区域为D,向区域D内随机投一点,则该点落入区域{(x,y)∈D|x2+y2<2}的概率是( )
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
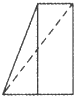
 如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )
如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )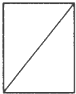


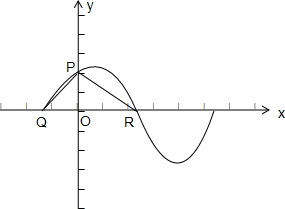 如图,点P(0,
如图,点P(0, 已知椭圆C1:
已知椭圆C1: