题目内容
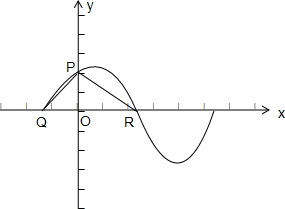 如图,点P(0,
如图,点P(0,| A |
| 2 |
| 2π |
| 3 |
(Ⅰ)求φ的值;
(Ⅱ)若PQ⊥PR,求A的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)由函数经过点P(0,
),可求得sinφ=
,φ∈[0,π),且点P在递增区间上可求得φ=
;
(Ⅱ)由(I)可知y=Asin(
x+
),令y=0可求得x=-
或x=
,从而可得P、Q、R的坐标,利用PQ⊥PR,得
•
=-
+
A2=0,从而可求得A.
| A |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(Ⅱ)由(I)可知y=Asin(
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
| 5 |
| 4 |
| PQ |
| PR |
| 5 |
| 16 |
| 1 |
| 4 |
解答:
解:(I)∵函数经过点P(0,
),
∴Asinφ=
,
∴sinφ=
,…(3分)
又∵φ∈[0,π),且点P在递增区间上,
∴φ=
,…(7分)
(II)由(I)可知y=Asin(
x+
),
令y=0,得sin(
x+
)=0
∴
x+
=0,∴x=-
或x=
,∴Q(-
,0),R(
,0)…(11分)
又∵P(0,
),∴
=(-
,-
),
=(
,-
),
∵PQ⊥PR,∴
•
=-
+
A2=0,
解得:A=
…(14分)
| A |
| 2 |
∴Asinφ=
| A |
| 2 |
∴sinφ=
| 1 |
| 2 |
又∵φ∈[0,π),且点P在递增区间上,
∴φ=
| π |
| 6 |
(II)由(I)可知y=Asin(
| 2π |
| 3 |
| π |
| 6 |
令y=0,得sin(
| 2π |
| 3 |
| π |
| 6 |
∴
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
又∵P(0,
| A |
| 2 |
| PQ |
| 1 |
| 4 |
| A |
| 2 |
| PR |
| 5 |
| 4 |
| A |
| 2 |
∵PQ⊥PR,∴
| PQ |
| PR |
| 5 |
| 16 |
| 1 |
| 4 |
解得:A=
| ||
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查向量的坐标运算,求得P、Q、R的坐标是关键,着重考查向量的数量积的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
按如图程序框图运算:若x=4,则运算进行几次才停止?( )


| A、3 | B、4 | C、5 | D、6 |

