题目内容
设曲线y=
与x轴所围成的区域为D,向区域D内随机投一点,则该点落入区域{(x,y)∈D|x2+y2<2}的概率是( )
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出对应区域的面积,利用几何概型的概率公式进行计算即可得到结论.
解答:
 解:y=
解:y=
与x轴所围成的区域为以C(1,0)为圆心半径为1的上半圆,面积SD=
π×12=
,
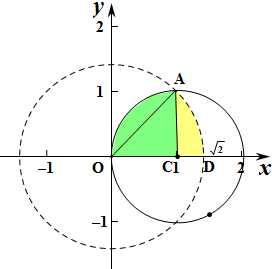
该点落入区域{(x,y)∈D|x2+y2<2}的区域如图:如图阴影部分,
则扇形AOC的面积S=
π×12=
,
三角形OAC的面积S△AOC=
×1×1=
,
扇形AOD的面积S=
×π(
)2=
,
则阴影部分的面积S阴影=S扇形AOC+S扇形AOD-S△AOC=
+
-
=
-
,
由几何概率的计算公式可得,该点落入区域{(x,y)∈D|x2+y2<2}的概率P=
=
=
,
故选A.
 解:y=
解:y=| 2x-x2 |
| 1 |
| 2 |
| π |
| 2 |
该点落入区域{(x,y)∈D|x2+y2<2}的区域如图:如图阴影部分,
则扇形AOC的面积S=
| 1 |
| 4 |
| π |
| 4 |
三角形OAC的面积S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
扇形AOD的面积S=
| 45 |
| 360 |
| 2 |
| π |
| 4 |
则阴影部分的面积S阴影=S扇形AOC+S扇形AOD-S△AOC=
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
由几何概率的计算公式可得,该点落入区域{(x,y)∈D|x2+y2<2}的概率P=
| S阴影 |
| SD |
| ||||
|
| π-1 |
| π |
故选A.
点评:本题主要考查了几何概型的概率计算以及扇形的面积公式的计算,要求熟练掌握扇形的面积公式和几何概型的概率公式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
阅读如图的流程图,若输入的a,b,c分别是5,2,6,则输出的a,b,c分别是( )


| A、6,5,2 |
| B、5,2,6 |
| C、2,5,6 |
| D、6,2,5 |
按如图程序框图运算:若x=4,则运算进行几次才停止?( )


| A、3 | B、4 | C、5 | D、6 |
非零向量
,
,|
|=m,|
|=n,若向量
=λ1
+λ2
,则|
|的最大值为( )
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| A、λ1m+λ2n |
| B、|λ1|m+|λ2|n |
| C、|λ1m+λ2n| |
| D、以上均不对 |
已知A(0,1),B(1,0),点C在抛物线y2=2x的图象上,若△ABC的面积大于
,则点C纵坐标的取值范围为( )
| 3 |
| 2 |
| A、(-4,2) |
| B、(-2,4) |
| C、(-∞,-4)∪(2,+∞) |
| D、(-∞,-2)∪(4,+∞) |
复数z1=1+bi,z2=-2+i,若
的实部和虚部互为相反数,则实数b的值为( )
| z1 |
| z2 |
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |