题目内容

1．已知复数z满足i•z=1-i（其中i为虚数单位），则|z|=$\sqrt{2}$．

分析 利用两个复数代数形式的乘除法，虚数单位i的幂运算性质，把复数化简到最简形式，利用复数的模的定义求出|z|．

解答 解：∵i•z=1-i（i为虚数单位），
∴z=$\frac{1-i}{i}$=$\frac{-i（1-i）}{{-i}^{2}}$=1-i，
∴|z|=$\sqrt{2}$，
故答案为：$\sqrt{2}$．

点评 本题考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，复数的模的定义和求法．

练习册系列答案
相关题目
11．在平面直角坐标系中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρ2（1+3sin2θ）=4，曲线C2：$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}$（θ为参数）．
（Ⅰ）求曲线C1的直角坐标方程和C2的普通方程；
（Ⅱ）极坐标系中两点A（ρ1，θ0），B（ρ2，θ0+$\frac{π}{2}$）都在曲线C1上，求$\frac{1}{ρ_1^2}$+$\frac{1}{ρ_2^2}$的值．
12．将90°化为弧度等于（　　）
A．$\frac{π}{4}$B．$\frac{π}{2}$C．πD．2π
9．已知数列{an}的递推公式an=$\frac{1}{{a}_{n-1}}$+an-1，且a1=1，请画出求其前5项的流程图．
16．已知数列$\{\frac{a_n}{n}\}$是等差数列，且a3=2，a15=30，则a9=（　　）
A．12B．24C．16D．32
6．函数f（a）=（3m-1）a+b-2m，当m∈[0，1]时，0≤f（a）≤1恒成立，则$\frac{{{b^2}-{a^2}}}{ab}$的范围是[0，$\frac{15}{4}$]．
13．已知函数f（x）=$\frac{1}{2}$ax2-2x+2lnx（a≥0），g（x）=x2+b，（b＞0）．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）当a=0时，若对任意x1，x2∈[$\frac{1}{e}$，e]，使|g（x2）-f（x1）|＜e2+4e成立，其中e=2.71828…，是自然对数的底数，求b的取值范围．
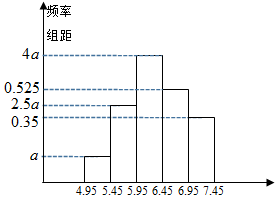10．质检部门抽查某批次产品的质量（单位：克），随机检查了其中80件产品，根据样本数据描绘的频率分布直方图如下：
（1）求频率分布直方图中a的值；
（2）若质量在[5.95，6.95）中的产品才算一级品，求在抽查的样本中一级产品共有多少件？
11．已知函数f（x）=a（lnx-2x2）-3x，a∈R．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）当a=-1时，函数g（x）=tx2-4x+1满足对任意的x1∈（0，e]，都存在x2∈[0，1]，使得f（x1）≥g（x2）成立，求实数t的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网