题目内容
已知函数f(x)=x-5+
(x>1)的最小值为n,则二项式(x-
)n展开式中x2项的系数为 ( )
| 25 |
| x-1 |
| 1 |
| x |
| A、15 | B、-15 |
| C、30 | D、-30 |
考点:二项式系数的性质
专题:二项式定理
分析:利用基本不等式求得f(x)的最小值n=6,在二项展开式的通项公式中,令x的幂指数等于2,求出r的值,即可求得二项式(x-
)6展开式中x2项的系数.
| 1 |
| x |
解答:
解:函数f(x)=x-5+
=(x-1)+
-4,由x>1,利用基本不等式可得f(x)≥2
-4=6,
当且仅当x-1=
,即x=6时,取等号,故f(x)的最小值为n=6,
则二项式(x-
)6展开式的通项公式为Tr+1=
•(-1)r•x6-2r,令6-2r=2,求得r=2,
故二项式(x-
)6展开式中x2项的系数为
=15,
故选:A.
| 25 |
| x-1 |
| 25 |
| x-1 |
| 25 |
当且仅当x-1=
| 25 |
| x-1 |
则二项式(x-
| 1 |
| x |
| C | r 6 |
故二项式(x-
| 1 |
| x |
| C | 2 6 |
故选:A.
点评:本题主要考查基本不等式,二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数x,y的约束条件为
,则x2+(y+2)2的取值范围是( )
|
A、(
| ||
| B、[1,5) | ||
C、(
| ||
| D、[1,17) |
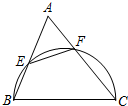 如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么
如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么