题目内容
△ABC中,顶点A(1,7),B(3,3),C(7,3),过B作BD⊥AC于D点,求D点坐标.
考点:直线的两点式方程,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:由A,C的坐标求出AC的斜率和方程,得到BD的斜率,由点斜式求出BD的方程,和AC的方程联立求交点得D的坐标.
解答:
解:∵A(1,7),C(7,3),
∴kAC=
=-
,
∴kBD=
,
又B(3,3),∴BD所在直线方程为:y-3=
(x-3),即3x-2y-3=0.
又AC所在直线方程为:
=
,即2x+3y-23=0.
联立
,解得
.
∴D点坐标为(
,
).
∴kAC=
| 7-3 |
| 1-7 |
| 2 |
| 3 |
∴kBD=
| 3 |
| 2 |
又B(3,3),∴BD所在直线方程为:y-3=
| 3 |
| 2 |
又AC所在直线方程为:
| y-3 |
| 7-3 |
| x-7 |
| 1-7 |
联立
|
|
∴D点坐标为(
| 55 |
| 13 |
| 126 |
| 13 |
点评:本题考查了直线的两点式方程,考查了直线的一般式方程与直线垂直的关系,是基础的计算题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数f(x)=x-5+
(x>1)的最小值为n,则二项式(x-
)n展开式中x2项的系数为 ( )
| 25 |
| x-1 |
| 1 |
| x |
| A、15 | B、-15 |
| C、30 | D、-30 |
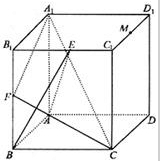 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1、B1B的中点,求证:CF⊥平面EAB.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1、B1B的中点,求证:CF⊥平面EAB.