题目内容
已知△ABC的三个顶点A(-1,0),B(1,0),C(3,2),其外接圆为圆H.对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M,N,使得点M是线段PN的中点,则圆C的半径r的取值范围是 .
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:设P的坐标,可得M的坐标,代入圆的方程,可得以(3,2)为圆心,r为半径的圆与以(6-m,4-n)为圆心,2r为半径的圆有公共点,由此求得⊙C的半径r的取值范围.
解答:
解:由题意,A(-1,0),B(1,0),C(3,2),
∴AB的垂直平分线是x=0,
∵BC:y=x-1,BC的中点是(2,1),
∴BC的垂直平分线是y=-x+3.
由
,得到圆心H是(0,3),∴r=
,
则直线BH的方程为3x+y-3=0,设P(m,n)(0≤m≤1),N(x,y).
因为点M是点P,N的中点,所以M(
,
),
又M,N都在半径为r的圆C上,所以
,
即
,
因为上式是关于x,y的方程组有解,
即以(3,2)为圆心,r为半径的圆,
与以(6-m,4-n)为圆心,2r为半径的圆有公共点,
所以(2r-r)2<(3-6+m)2+(2-4+n)2<(r+2r)2,
又3m+n-3=0,
所以r2<10m2-12m+10<9r2对任意m∈[0,1]成立.
而f(m)=10m2-12m+10在[0,1]上的值域为[
,10],
又线段BH与圆C无公共点,
所以(m-3)2+(3-3m-2)2>r2对任意m∈[0,1]成立,即r2<
.
10m2-12m+10<9r2对任意m∈[0,1]成立,则有r2>
,
故圆C的半径r的取值范围为(
,
).
故答案为:(
,
).
∴AB的垂直平分线是x=0,
∵BC:y=x-1,BC的中点是(2,1),
∴BC的垂直平分线是y=-x+3.
由
|
| 10 |
则直线BH的方程为3x+y-3=0,设P(m,n)(0≤m≤1),N(x,y).
因为点M是点P,N的中点,所以M(
| m+x |
| 2 |
| n+y |
| 2 |
又M,N都在半径为r的圆C上,所以
|
即
|
因为上式是关于x,y的方程组有解,
即以(3,2)为圆心,r为半径的圆,
与以(6-m,4-n)为圆心,2r为半径的圆有公共点,
所以(2r-r)2<(3-6+m)2+(2-4+n)2<(r+2r)2,
又3m+n-3=0,
所以r2<10m2-12m+10<9r2对任意m∈[0,1]成立.
而f(m)=10m2-12m+10在[0,1]上的值域为[
| 32 |
| 5 |
又线段BH与圆C无公共点,
所以(m-3)2+(3-3m-2)2>r2对任意m∈[0,1]成立,即r2<
| 32 |
| 5 |
10m2-12m+10<9r2对任意m∈[0,1]成立,则有r2>
| 10 |
| 9 |
故圆C的半径r的取值范围为(
| ||
| 3 |
4
| ||
| 5 |
故答案为:(
| ||
| 3 |
4
| ||
| 5 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查解不等式,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
设F1、F2是双曲线
-
=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|、|PF2|的等差中项为
,|PF1|、|PF2|的等比中项为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3b |
| 2 |
| 3 |
| 2 |
| ab |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=x-5+
(x>1)的最小值为n,则二项式(x-
)n展开式中x2项的系数为 ( )
| 25 |
| x-1 |
| 1 |
| x |
| A、15 | B、-15 |
| C、30 | D、-30 |
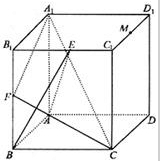 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1、B1B的中点,求证:CF⊥平面EAB.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1、B1B的中点,求证:CF⊥平面EAB.