题目内容

y=（3a-1）x+2，在（-∞，+∞）上是减函数，则a的取值范围是（　　）
A、(-∞，
1
3
)
B、[
1
3
，+∞)
C、(
1
3
，+∞)
D、（ -∞，
1
3
]
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：根据一次函数的图象与性质，求出a的取值范围．
解答： 解：∵函数y=（3a-1）x+2，在（-∞，+∞）上是减函数，
∴3a-1＜0，
解得a＜
1
3
；
∴a的取值范围是（-∞，
1
3
）．
故选：A．
点评：本题考查了一次函数的图象与性质的应用问题，解题时应熟记常见的函数的图象与性质，是基础题．
练习册系列答案
相关题目
已知log
1
2
b＜log
1
2
a＜0＜c＜1，则（　　）
A、2b＞2a＞2c
B、2a＞2b＞2c
C、2c＞2b＞2a
D、2c＞2a＞2b
已知集合A={x|x-m=0}，B={x|1-3x＞-2}，且 A∩B=∅，则实数m满足的条件是
 
．
已知f（x）是偶函数，且x＞0时，f（x）=x2+ax，若f（-1）=2，则f（2）的值是（　　）
A、-1B、1C、3D、6
已知向量
a
=（1，2），
b
=（6，k），且
a
∥
b
，则k=
 
．
求函数y=
6-5x-x2
的定义域及值域．
已知集合M={a，0}，N={1，2}，且M∩N={1}，那么M∪N的真子集有
 
个．
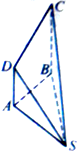如图，在四棱锥S-ABCD中，DA⊥平面SAB，BC⊥平面SAB，AB=BC=SA=2AD=2，∠BAS=120°．
（1）求证：平面SCD⊥平面SBC；
（2）求平面SAD与平面SBC所成锐角二面角的余弦值．
解不等式：(1-
3
4
)x≤
1
100
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网