题目内容
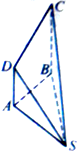 如图,在四棱锥S-ABCD中,DA⊥平面SAB,BC⊥平面SAB,AB=BC=SA=2AD=2,∠BAS=120°.
如图,在四棱锥S-ABCD中,DA⊥平面SAB,BC⊥平面SAB,AB=BC=SA=2AD=2,∠BAS=120°.(1)求证:平面SCD⊥平面SBC;
(2)求平面SAD与平面SBC所成锐角二面角的余弦值.
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)要证明平面SCD⊥平面SBC,根据面面垂直的判定定理,只要在平面SCD内找一直线垂直于平面SBC即可.取SC中点E,SB中点F,连接DE,EF,FA,则通过图形容易看到DE就是所找直线,容易说明AF⊥SB,AF⊥BC,所以DE⊥SB,DE⊥BC,SB∩BC=B,所以DE⊥平面SBC,DE?平面SCD,所以平面SCD⊥平面SBC;
(2)由(1)知AF⊥平面SBC,过F作FG⊥SA,垂足为G,因为DA⊥平面SAB,所以DA⊥FG,即FG⊥DA,所以FG⊥平面SAD,所以AF与FG的夹角等于平面SAD与平面SBC所成锐角二面角,所以在Rt△AFG中,求出边AF,FG的长度,便可求出cos∠AFG.
(2)由(1)知AF⊥平面SBC,过F作FG⊥SA,垂足为G,因为DA⊥平面SAB,所以DA⊥FG,即FG⊥DA,所以FG⊥平面SAD,所以AF与FG的夹角等于平面SAD与平面SBC所成锐角二面角,所以在Rt△AFG中,求出边AF,FG的长度,便可求出cos∠AFG.
解答:
解:(1)如图,取SC中点E,SB中点F,连接DE,EF,FA,则:
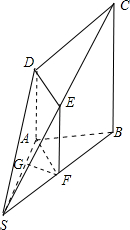 EF∥BC,且EF=
EF∥BC,且EF=
BC,∵DA⊥平面SAB,BC⊥平面SAB,∴DA∥BC,∴EF∥DA,EF=DA;
∴四边形ADEF是平行四边形,∴DE∥AF;
∵AB=SA,F是SB中点,∴AF⊥SB;
又BC⊥平面SAB,AF?平面SAB,∴BC⊥AF,即AF⊥BC;
即AF⊥SB,AF⊥BC,∴DE⊥SB,DE⊥BC,SB∩BC=B;
∴DE⊥平面SBC,DE?平面SCD;
∴平面SCD⊥平面SBC;
(2)由(1)知AF⊥平面SBC,过F作FG⊥SA,交SA于G;
∵DA⊥平面SAB,FG?平面SAB;
∴DA⊥FG,即FG⊥DA,SA∩DA=A;
∴FG⊥平面SAD,∴∠AFG等于平面SAD与平面SBC所成锐角二面角;
在Rt△SAF中,SA=2,∠BAS=120°,∴∠ASB=30°,∴AF=1;
∴在Rt△SFG中,FG=
SF=
;
∴cos∠AFG=
=
=
;
∴平面SAD与平面SBC所成锐角二面角的余弦值为
.
 EF∥BC,且EF=
EF∥BC,且EF=| 1 |
| 2 |
∴四边形ADEF是平行四边形,∴DE∥AF;
∵AB=SA,F是SB中点,∴AF⊥SB;
又BC⊥平面SAB,AF?平面SAB,∴BC⊥AF,即AF⊥BC;
即AF⊥SB,AF⊥BC,∴DE⊥SB,DE⊥BC,SB∩BC=B;
∴DE⊥平面SBC,DE?平面SCD;
∴平面SCD⊥平面SBC;
(2)由(1)知AF⊥平面SBC,过F作FG⊥SA,交SA于G;
∵DA⊥平面SAB,FG?平面SAB;
∴DA⊥FG,即FG⊥DA,SA∩DA=A;
∴FG⊥平面SAD,∴∠AFG等于平面SAD与平面SBC所成锐角二面角;
在Rt△SAF中,SA=2,∠BAS=120°,∴∠ASB=30°,∴AF=1;
∴在Rt△SFG中,FG=
| 1 |
| 2 |
| ||
| 2 |
∴cos∠AFG=
| FG |
| AF |
| ||||
| 1 |
| ||
| 2 |
∴平面SAD与平面SBC所成锐角二面角的余弦值为
| ||
| 2 |
点评:考查线面垂直的性质,中卫线的性质,线面垂直的判定定理,面面垂直的判定定理,以及二面角的概念.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
y=(3a-1)x+2,在(-∞,+∞)上是减函数,则a的取值范围是( )
A、(-∞,
| ||
B、[
| ||
C、(
| ||
D、( -∞,
|
函数f(x)=
(x>0)的值域为( )
| 2x-1 |
| x+1 |
| A、(-∞,2) |
| B、(-∞,2)∪(2,+∞) |
| C、[-1,2] |
| D、(-1,2) |