题目内容
椭圆的中心在原点，准线方程为x=±
，长轴长为6的椭圆方程为（ ）
| 9 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出a，b，c分别为椭圆的半长轴，半短轴及焦距的一半，根据椭圆的准线方程公式列出a与c的方程记作①，根据长轴长为6列出a的方程记作②，联立①②即可求出a与c的值，根据a2=b2+c2即可求出b的值，由椭圆的中心在原点，利用a与b的值写出椭圆的标准方程即可．
解答：
解：设a为半长轴，b为半短轴，c为焦距的一半，
根据题意可知：
=
即a2=
c①，2a=6②，
把②代入①解得：c=2，a=3，所以b=
，
又椭圆的中心在原点，则所求椭圆的方程为：
+
=1．
故选：B．
根据题意可知：
| a2 |
| c |
| 9 |
| 2 |
| 9 |
| 2 |
把②代入①解得：c=2，a=3，所以b=
| 5 |
又椭圆的中心在原点，则所求椭圆的方程为：
| x2 |
| 9 |
| y2 |
| 5 |
故选：B．
点评：此题考查学生灵活运用椭圆的准线方程及离心率的公式化简求值，掌握椭圆的一些基本性质，是一道综合题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在数列{an}中，如果a1=1，且an+1=
an，则a3等于（ ）
| 1 |
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
已知集合A={x|x=
+
π，k∈Z}，B={x|x=
+
π，k∈Z}，则（ ）
| kπ |
| 2 |
| 1 |
| 4 |
| kπ |
| 4 |
| 1 |
| 2 |
| A、A=B | B、A?B |
| C、A?B | D、A∩B=∅ |
已知函数f（x）=
的定义域为R，则实数a的取值范围是（ ）
| x+1 |
| a2x-2x+a |
| A、a＜-1或a＞1 |
| B、a＞1 |
| C、a＜-1 |
| D、a＞1或a=0或a＜-1 |
已知椭圆的焦点F1、F2在x轴上，它与y轴的一个交点为P，且△PF1F2为正三角形，且椭圆上的点与焦点的最短距离为
，则椭圆的方程为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
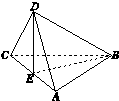已知正方形ABCD的对角线AC与BD相交于E点，将△ABC沿对角线AC折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的为（ ）| A、直线AB⊥直线CD，且直线AC⊥直线BD |
| B、直线AB⊥平面BCD，且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE，且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD，且平面ACD⊥平面BDE |
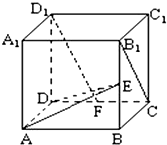在正方体ABCD-A1B1C1D1中，如图E、F分别是BB1，CD的中点．