题目内容
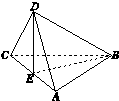 已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )| A、直线AB⊥直线CD,且直线AC⊥直线BD |
| B、直线AB⊥平面BCD,且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE,且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
考点:平面与平面垂直的性质
专题:空间位置关系与距离
分析:由直线AB⊥直线CD不成立,知A错误;由直线AB⊥平面BCD不成立,知B错误;由平面ABC⊥平面BDE,且平面ACD⊥平面BDE,知C正确;由平面ABD⊥平面BCD不成立,知D错误.
解答:
解:由题意知DC⊥BE,AB∩BE=E,
∴直线AB⊥直线CD不成立,故A错误;
∵AC⊥AB,∴AB与BC不垂直,
∴直线AB⊥平面BCD不成立,故B错误;
∵BE⊥DE,BE⊥AC,∴AC⊥平面BDE,
∴平面ABC⊥平面BDE,且平面ACD⊥平面BDE,故C正确;
∵平面ABD⊥平面BCD不成立,故D错误.
故选:C.
∴直线AB⊥直线CD不成立,故A错误;
∵AC⊥AB,∴AB与BC不垂直,
∴直线AB⊥平面BCD不成立,故B错误;
∵BE⊥DE,BE⊥AC,∴AC⊥平面BDE,
∴平面ABC⊥平面BDE,且平面ACD⊥平面BDE,故C正确;
∵平面ABD⊥平面BCD不成立,故D错误.
故选:C.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={x|-3≤2x-1≤3},集合B为函数y=lg(x-1)-2sinx的定义域,则A∩B=( )
| A、(1,2) |
| B、[1,2] |
| C、[1,2) |
| D、(1,2] |
已知角α的终边上一点P(3,m),且cosα=
,则m=( )
| 3 |
| 5 |
| A、4 | B、-4 | C、±4 | D、±5 |
椭圆的中心在原点,准线方程为x=±
,长轴长为6的椭圆方程为( )
| 9 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
点(1,2)在圆
的( )
|
| A、内部 | B、外部 |
| C、圆上 | D、与θ的值有关 |