题目内容
已知数列{an}中,a1=3,an+1+an=3•2n,n∈N*.
(1)证明数列{an-2n}是等比数列,并求数列{an}的通项公式;
(2)在数列{an}中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若1<r<s且r,s∈N*,求证:使得a1,ar,as成等差数列的点列(r,s)在某一直线上.
(1)证明数列{an-2n}是等比数列,并求数列{an}的通项公式;
(2)在数列{an}中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若1<r<s且r,s∈N*,求证:使得a1,ar,as成等差数列的点列(r,s)在某一直线上.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)将条件变形,构造符合条件的数列,即可证明数列{an-2n}是等比数列,从而可求数列{an}的通项公式;
(2)假设在数列{an}中存在连续三项成等差数列,代入相应的项,化简可得结论;
(3)若a1,ar,as成等差数列,则2ar=a1+as,代入变形整理,对r、s进行讨论,可得结论.
(2)假设在数列{an}中存在连续三项成等差数列,代入相应的项,化简可得结论;
(3)若a1,ar,as成等差数列,则2ar=a1+as,代入变形整理,对r、s进行讨论,可得结论.
解答:
(1)证明:将已知条件an+1+an=3•2n变形为an+1-2n+1=-(an-2n)…(1分)
由于a1-2=3-2=1≠0,则
=-1(常数)…(3分)
即数列{an-2n}是以1为首项,公比为-1的等比数列…(4分)
所以an-2n=1•(-1)n-1=(-1)n-1,即an=2n+(-1)n-1(n∈N*).…(5分)
(2)解:假设在数列{an}中存在连续三项成等差数列,不妨设连续的三项依次为ak-1,ak,ak+1(k≥2,k∈N*),由题意得,2ak=ak-1+ak+1,
将ak=2k+(-1)k-1,ak-1=2k-1+(-1)k-2,ak+1=2k+1+(-1)k代入上式得…(7分)
2[2k+(-1)k-1]=[2k-1+(-1)k-2]+[2k+1+(-1)k]…(8分)
化简得,-2k-1=4•(-1)k-2,即2k-1=4•(-1)k-1,得(-2)k-1=4,解得k=3,
所以,存在满足条件的连续三项为a2,a3,a4成等比数列.…(10分)
(3)证明:若a1,ar,as成等差数列,则2ar=a1+as,
即2[2r+(-1)r-1]=3+2s+(-1)s-1,变形得2s-2r+1=2•(-1)r-1-(-1)s-1-3…(11分)
由于若r,s∈N*且1<r<s,下面对r、s进行讨论:
①若r,s均为偶数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
②若r为奇数,s为偶数,则2s-2r+1=0,解得s=r+1;
③若r为偶数,s为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
④若r,s均为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;…(15分)
综上①②③④可知,只有当r为奇数,s为偶数时,a1,ar,as成等差数列,
此时满足条件点列(r,s)落在直线y=x+1(其中
∈(1, 2]为正奇数)上.…(16分)(不写出直线方程扣1分)
由于a1-2=3-2=1≠0,则
| an+1-2n+1 |
| an-2n |
即数列{an-2n}是以1为首项,公比为-1的等比数列…(4分)
所以an-2n=1•(-1)n-1=(-1)n-1,即an=2n+(-1)n-1(n∈N*).…(5分)
(2)解:假设在数列{an}中存在连续三项成等差数列,不妨设连续的三项依次为ak-1,ak,ak+1(k≥2,k∈N*),由题意得,2ak=ak-1+ak+1,
将ak=2k+(-1)k-1,ak-1=2k-1+(-1)k-2,ak+1=2k+1+(-1)k代入上式得…(7分)
2[2k+(-1)k-1]=[2k-1+(-1)k-2]+[2k+1+(-1)k]…(8分)
化简得,-2k-1=4•(-1)k-2,即2k-1=4•(-1)k-1,得(-2)k-1=4,解得k=3,
所以,存在满足条件的连续三项为a2,a3,a4成等比数列.…(10分)
(3)证明:若a1,ar,as成等差数列,则2ar=a1+as,
即2[2r+(-1)r-1]=3+2s+(-1)s-1,变形得2s-2r+1=2•(-1)r-1-(-1)s-1-3…(11分)
由于若r,s∈N*且1<r<s,下面对r、s进行讨论:
①若r,s均为偶数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
②若r为奇数,s为偶数,则2s-2r+1=0,解得s=r+1;
③若r为偶数,s为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;
④若r,s均为奇数,则2s-2r+1<0,解得s<r+1,与1<r<s矛盾,舍去;…(15分)
综上①②③④可知,只有当r为奇数,s为偶数时,a1,ar,as成等差数列,
此时满足条件点列(r,s)落在直线y=x+1(其中
| 2 |
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项,考查分类讨论的数学思想,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
已知x,y满足(x-1)2+y2=16,则x2+y2的最小值为( )
| A、3 | B、5 | C、9 | D、25 |
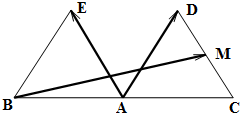 如图,△ABE与△ACD都是正三角形,且
如图,△ABE与△ACD都是正三角形,且| BA |
| AC |
| CM |
| MD |
| BM |
| AE |
| AD |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
抛一枚均匀硬币,正,反面出现的概率都是
,反复投掷,数列{an}定义:an=
,若Sn=a1+a2+…+an(n∈N•),则事件S4>0的概率为( )
| 1 |
| 2 |
|
A、
| ||
B、
| ||
C、
| ||
D、
|
将一根长为3m的木棒随机折成三段,折成的这三段木棒能够围成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|