题目内容
已知向量
=（a，b），
=（sin2x，2cos2x），若f（x）=
•
，且f(0)=8，f(
)=12．
（1）求a，b的值；
（2）求函数f（x）的最大值及取得最大值时的x的集合；
（3）求函数f（x）的单调增区间．
| m |
| n |
| m |
| n |
| π |
| 6 |
（1）求a，b的值；
（2）求函数f（x）的最大值及取得最大值时的x的集合；
（3）求函数f（x）的单调增区间．
考点：三角函数中的恒等变换应用,平面向量数量积的运算
专题：三角函数的图像与性质
分析：（1）由题意可知f（x）=asin2x+2bcos2x．由f（0）=2b=8，解得b．再利用f(
)=asin
+2bcos2
=
a+8×
=12，解得a即可．
（2）由（1）可知f(x)=4
sin2x+4cos2x+4，利用两角和的直线公式可得f(x)=8sin(2x+
)+4．当2x+
=2kπ+
，k∈Z时，sin(2x+
)取得最大值1，即可得出f（x）max．
（3）利用正弦函数的单调性即可得出．
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| 4 |
（2）由（1）可知f(x)=4
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
（3）利用正弦函数的单调性即可得出．
解答：
解：（1）由题意可知f（x）=asin2x+2bcos2x
由f（0）=2b=8，解得b=4．
由f(
)=asin
+2bcos2
=
a+8×
=12，解得a=4
．
（2）由（1）可知f(x)=4
sin2x+4cos2x+4=8(
sin2x+
cos2x)+4
∴f(x)=8sin(2x+
)+4．
当2x+
=2kπ+
，k∈Z时，sin(2x+
)取得最大值1，
∴f（x）max=8×1+4=12
此时x的集合为{x|x=kπ+
，k∈Z}．
（3）由-
+2kπ≤2x+
≤2kπ+
（k∈Z），
解得kπ-
≤x≤kπ+
（k∈Z）．
∴函数f（x）的单调增区间是[kπ-
，kπ+
]（k∈Z）．
由f（0）=2b=8，解得b=4．
由f(
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
（2）由（1）可知f(x)=4
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴f(x)=8sin(2x+
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
∴f（x）max=8×1+4=12
此时x的集合为{x|x=kπ+
| π |
| 6 |
（3）由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| π |
| 3 |
| π |
| 6 |
∴函数f（x）的单调增区间是[kπ-
| π |
| 3 |
| π |
| 6 |
点评：本题考查了三角函数的图象与性质、两角和的正弦公式等基础知识与基本技能方法，属于中档题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知命题p：?x∈R，有3x＜2x成立；命题q：?x∈（0，+∞），恒有sinx+
≥2成立，则下列命题为真命题的是（ ）
| 1 |
| sinx |
| A、p∧q |
| B、（￢p）∨q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
已知定义在R上的函数f（x）是偶函数，对于任意x∈R，当x≥0都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log2（x+1），则f（-2013）+f（2014）的值为（ ）
| A、2 | B、1 | C、-1 | D、-2 |
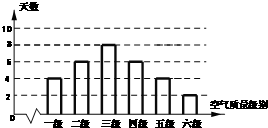根据空气质量指数AQI（为整数）的不同，可将空气质量分级如下表：已知函数f(x)=
，则f[f(
)]等于（ ）
|
| 5 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、
|