题目内容
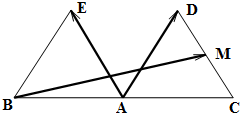 如图,△ABE与△ACD都是正三角形,且
如图,△ABE与△ACD都是正三角形,且| BA |
| AC |
| CM |
| MD |
| BM |
| AE |
| AD |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:先根据△ABE与△ACD都是正三角形,且
=
,则
=
,然后根据平面向量基本定理将
用
与
表示,从而求出λ,μ的值,即可求出所求.
| BA |
| AC |
| AE |
| CD |
| BM |
| AE |
| AD |
解答:
解:∵△ABE与△ACD都是正三角形,且
=
,
∴
=
,而
=
,
∴
=
+
=2
+
=2(
-
)+
=-
+2
,
∵
=λ
+μ
,
∴λ=-
,μ=2,则λμ=-
×2=-3.
故选:B.
| BA |
| AC |
∴
| AE |
| CD |
| CM |
| MD |
∴
| BM |
| BC |
| CM |
| AC |
| 1 |
| 2 |
| CD |
| AD |
| CD |
| 1 |
| 2 |
| CD |
| 3 |
| 2 |
| AE |
| AD |
∵
| BM |
| AE |
| AD |
∴λ=-
| 3 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题主要考查了向量在几何中的应用,以及平面向量基本定理的应用,同时考查了转化的思想和运算的能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=(x2-1)
的零点个数是( )
| x2-4 |
| A、1 | B、2 | C、3 | D、4 |
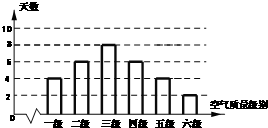 根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表: