题目内容
点（1，2）在圆
的（ ）
|
| A、内部 | B、外部 |
| C、圆上 | D、与θ的值有关 |
考点：圆的参数方程
专题：坐标系和参数方程
分析：把圆的参数方程化为直角坐标方程，求得点（1，2）到圆心的距离大于半径，可得此点在圆的外部．
解答：
解：圆
，即 （x+1）2+y2=4，表示以（-1，0）为圆心、半径等于2的圆．
点（1，2）到圆心的距离为 2
，大于半径，故此点在圆的外部，
故选：B．
|
点（1，2）到圆心的距离为 2
| 2 |
故选：B．
点评：本题主要考查把参数方程化为直角坐标方程的方法，点和圆的位置关系，属于基础题．
练习册系列答案
相关题目
设复数z=
（i为虚数单位），则z的虚部为（ ）
| 2 |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
已知f（n）=
，且an=f（n）+f（n+1），则a1+a2+…+a2014的值为（ ）
|
| A、0 | B、2014 |
| C、-2014 | D、2014×2015 |
已知函数f（x）=
的定义域为R，则实数a的取值范围是（ ）
| x+1 |
| a2x-2x+a |
| A、a＜-1或a＞1 |
| B、a＞1 |
| C、a＜-1 |
| D、a＞1或a=0或a＜-1 |
已知x与y之间的一组数据：
则y与x的线性回归方程为
=bx+a必过点（ ）
| x | 1 | 2 | 3 | 4 |
| y | 2 | 3 | 5 | 8 |
 |
| y |
| A、（4.5，2.5） |
| B、（1.5，4.5） |
| C、（2.5，4.5） |
| D、（1.5，4） |
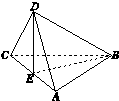已知正方形ABCD的对角线AC与BD相交于E点，将△ABC沿对角线AC折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的为（ ）| A、直线AB⊥直线CD，且直线AC⊥直线BD |
| B、直线AB⊥平面BCD，且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE，且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD，且平面ACD⊥平面BDE |