题目内容
已知
=3
-4
，
+
=4
-3
，
与
为相互垂直的单位向量．
（1）求向量
，
的夹角；
（2）对非零向量
，
，如果存在不为零的常数α，β使α
+β
=
，那么称向量
，
是线性相关的，否则称向量
，
是线性无关的．向量
，
是线性相关还是线性无关？为什么？
| a |
| i |
| j |
| a |
| b |
| i |
| j |
| i |
| j |
（1）求向量
| a |
| b |
（2）对非零向量
| p |
| q |
| p |
| q |
| 0 |
| p |
| q |
| p |
| q |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由题意求得
=
+
，可得|
|、|
|、
•
的值，再由 cos＜
，
＞=
求得＜
，
＞的值．
（2）设α•
+β•
=0，求得α=β=0，从而得出结论．
| b |
| i |
| j |
| a |
| b |
| a |
| b |
| a |
| b |
| ||||
|
|
| a |
| b |
（2）设α•
| a |
| b |
解答：
解：（1）由题意知
=3
-4
，
+
=4
-3
可得
=4
-3
-
=
+
，
∴|
|=
=5，|
|=
，
•
=（3
-4
）•（
+
）=-1，
∴cos＜
，
＞=
=
=-
，∴＜
，
＞=π-arccos
．
（2）设α•
+β•
=0，可得α（3
-4
）+β（
+
）=0，
即 （3α+β）
+（β-4α）
=0，∴
，解得α=β=0，
故不存在不为零的常数α，β使α
+β
=
，故向量
，
是线性无关．
| a |
| i |
| j |
| a |
| b |
| i |
| j |
| b |
| i |
| j |
| a |
| i |
| j |
∴|
| a |
| 9+16 |
| b |
| 2 |
| a |
| b |
| i |
| j |
| i |
| j |
∴cos＜
| a |
| b |
| ||||
|
|
| -1 | ||
5
|
| ||
| 10 |
| a |
| b |
| ||
| 10 |
（2）设α•
| a |
| b |
| i |
| j |
| i |
| j |
即 （3α+β）
| i |
| j |
|
故不存在不为零的常数α，β使α
| a |
| b |
| 0 |
| a |
| b |
点评：本题主要考查用两个向量的数量积表示两个向量的夹角，两个向量线性相关的定义，属于基础题．
练习册系列答案
相关题目
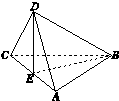已知正方形ABCD的对角线AC与BD相交于E点，将△ABC沿对角线AC折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的为（ ）| A、直线AB⊥直线CD，且直线AC⊥直线BD |
| B、直线AB⊥平面BCD，且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE，且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD，且平面ACD⊥平面BDE |