题目内容
设集合A={x|-3≤2x-1≤3}，集合B为函数y=lg（x-1）-2sinx的定义域，则A∩B=（ ）
| A、（1，2） |
| B、[1，2] |
| C、[1，2） |
| D、（1，2] |
考点：交集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，求出B中函数的定义域确定出B，找出A与B的交集即可．
解答：
解：由A中不等式解得：-1≤x≤2，即A=[-1，2]；
由B中函数得：x-1＞0，
解得：x＞1，即B=（1，+∞），
则A∩B=（1，2]．
故选：D．
由B中函数得：x-1＞0，
解得：x＞1，即B=（1，+∞），
则A∩B=（1，2]．
故选：D．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
在椭圆 在数列{an}中，如果a1=1，且an+1=
an，则a3等于（ ）
| 1 |
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
设复数z=
（i为虚数单位），则z的虚部为（ ）
| 2 |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
已知集合A={x|y=
}，B={y|y=2x，x＞0}，则A∪B=（ ）
| 9-x2 |
| A、{x|x＞1} |
| B、{x|1＜x≤3} |
| C、{x|x≥-3} |
| D、∅ |
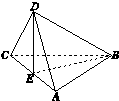已知正方形ABCD的对角线AC与BD相交于E点，将△ABC沿对角线AC折起，使得平面ABC⊥平面ADC（如图），则下列命题中正确的为（ ）| A、直线AB⊥直线CD，且直线AC⊥直线BD |
| B、直线AB⊥平面BCD，且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE，且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD，且平面ACD⊥平面BDE |