题目内容
数列{an}满足a1=1,an+1
=1,记Sn=a12+a22+a32+…+an2,若S2n-1-Sn≤
对任意n∈N*恒成立,则正整数m的最小值是 .
|
| m |
| 30 |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出{
}是首项为1,公差为4的等差数列,从而an2=
,并推导出数列{S2n+1-Sn}(n∈N*)是递减数列,由此能求出m的最小值为10.
| 1 |
| an2 |
| 1 |
| 4n-3 |
解答:
解:∵an+1
=1,∴an+12(
+4)=1,
∴
=
+4(n∈N*),又a1=1,
=1
∴{
}是首项为1,公差为4的等差数列,
∴
=1+4(n-1)=4n-3,∴an2=
∵(S2n+1-Sn)-(S2n+3-Sn+1)
=(an+12+an+22+…+a2n+12)-(an+22+an+32+…+a2n+32)
=an+12-a2n+22-a2n+32
=
-
-
=(
-
)+(
-
)>0,
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为
S3-S1=a22+a32=
+
=
,
∵
≤
,∴m≥
,
又∵m是正整数,∴m的最小值为10.
故答案为:10.
|
| 1 |
| an2 |
∴
| 1 |
| an+12 |
| 1 |
| an2 |
| 1 |
| a12 |
∴{
| 1 |
| an2 |
∴
| 1 |
| an2 |
| 1 |
| 4n-3 |
∵(S2n+1-Sn)-(S2n+3-Sn+1)
=(an+12+an+22+…+a2n+12)-(an+22+an+32+…+a2n+32)
=an+12-a2n+22-a2n+32
=
| 1 |
| 4n+1 |
| 1 |
| 8n+5 |
| 1 |
| 8n+9 |
=(
| 1 |
| 8n+2 |
| 1 |
| 8n+5 |
| 1 |
| 8n+2 |
| 1 |
| 8n+9 |
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为
S3-S1=a22+a32=
| 1 |
| 5 |
| 1 |
| 9 |
| 14 |
| 45 |
∵
| 14 |
| 45 |
| m |
| 30 |
| 28 |
| 3 |
又∵m是正整数,∴m的最小值为10.
故答案为:10.
点评:本题考查实数的最小值的求法,是中档题,解题时要认真审题,注意数列的通项公式和单调性的灵活运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知集合A={x|x=
+
π,k∈Z},B={x|x=
+
π,k∈Z},则( )
| kπ |
| 2 |
| 1 |
| 4 |
| kπ |
| 4 |
| 1 |
| 2 |
| A、A=B | B、A?B |
| C、A?B | D、A∩B=∅ |
已知椭圆的焦点F1、F2在x轴上,它与y轴的一个交点为P,且△PF1F2为正三角形,且椭圆上的点与焦点的最短距离为
,则椭圆的方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
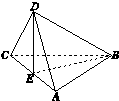 已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )| A、直线AB⊥直线CD,且直线AC⊥直线BD |
| B、直线AB⊥平面BCD,且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE,且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
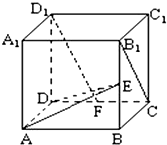 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.