题目内容
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=an•log
an,Sn=b1+b2+…+bn,求使Sn+n•2n+1>50成立的正整数n的最小值.
(1)求数列{an}的通项公式;
(2)若bn=an•log
| 1 |
| 2 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)设等比数列{an}的首项为a1,公比为q,依题意,可得到关于a1与q的方程组,解之即可求得数列{an}的通项公式;
(2)(1)得an=2n,再由bn=an•log
an,可得bn=-n•2n,于是Sn=-(1×2+2×22+…+n•2n),利用错位相减法即可求得Sn=2+22+23+…+2n-n•2n+1=2n+1-2-n•2n+1
,解不等式Sn+n•2Pn+1P>50即可求得使之成立的正整数n的最小值.
(2)(1)得an=2n,再由bn=an•log
| 1 |
| 2 |
,解不等式Sn+n•2Pn+1P>50即可求得使之成立的正整数n的最小值.
解答:
解:(1)设等比数列{an}的首项为a1,公比为q.
依题意,有2(a3+2)=a2+a4,代入a2+a3+a4=28,
可得a3=8,∴a2+a4=20,…(2分)
即
,解之得
或
…(4分)
又∵数列{an}单调递增,所以q=2,a1=2,
∴数列{an}的通项公式为an=2n. …(6分)
(2)因为bn=2nlog
2n=-n•2n,
所以Sn=-(1×2+2×22+…+n•2n),
2Sn=-[1×22+2×23+…+(n-1)•2n+n•2n+1],
两式相减,得Sn=2+22+23+…+2n-n•2n+1=2n+1-2-n•2n+1. …(10分)
要使Sn+n•2n+1>50,即2n+1-2>50,即2n+1>52.
易知:当n≤4时,2n+1≤25=32<52;
当n≥5时,2n+1≥26=64>52.故使
Sn+n•2n+1>50成立的正整数n的最小值为5.…(12分)
依题意,有2(a3+2)=a2+a4,代入a2+a3+a4=28,
可得a3=8,∴a2+a4=20,…(2分)
即
|
|
|
又∵数列{an}单调递增,所以q=2,a1=2,
∴数列{an}的通项公式为an=2n. …(6分)
(2)因为bn=2nlog
| 1 |
| 2 |
所以Sn=-(1×2+2×22+…+n•2n),
2Sn=-[1×22+2×23+…+(n-1)•2n+n•2n+1],
两式相减,得Sn=2+22+23+…+2n-n•2n+1=2n+1-2-n•2n+1. …(10分)
要使Sn+n•2n+1>50,即2n+1-2>50,即2n+1>52.
易知:当n≤4时,2n+1≤25=32<52;
当n≥5时,2n+1≥26=64>52.故使
Sn+n•2n+1>50成立的正整数n的最小值为5.…(12分)
点评:本题考查数列的求和,着重考查等比数列的通项公式的应用,突出考查错位相减法求和,考查运算、分析、求解的能力,属于中档题.

练习册系列答案
相关题目
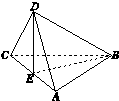 已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ABC沿对角线AC折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的为( )| A、直线AB⊥直线CD,且直线AC⊥直线BD |
| B、直线AB⊥平面BCD,且直线AC⊥平面BDE |
| C、平面ABC⊥平面BDE,且平面ACD⊥平面BDE |
| D、平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
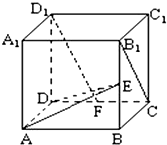 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.