题目内容
2.已知f(x)=x+xlnx,若k(x-2)<f(x)对任意x>2恒成立,则整数k的最大值是( )| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
分析 问题转化为k<$\frac{f(x)}{x-2}$=$\frac{x+xlnx}{x-2}$;令F(x)=$\frac{x+xlnx}{x-2}$,根据函数的单调性得到存在x0∈(8,9),使g(x0)=0,即2lnx0=x0-4;求出F(x)的最小值,从而求出k的最大值即可.
解答 解:∵x>2,
∴k(x-2)<f(x)可化为k<$\frac{f(x)}{x-2}$=$\frac{x+xlnx}{x-2}$;
令F(x)=$\frac{x+xlnx}{x-2}$,
则F′(x)=$\frac{x-2lnx-4}{{(x-2)}^{2}}$;
令g(x)=x-2lnx-4,则g′(x)=1-$\frac{2}{x}$>0,
故g(x)在(2,+∞)上是增函数,
且g(8)=8-2ln8-4=2(2-ln8)<0,g(9)=9-2ln9-4=5-2ln9>0;
故存在x0∈(8,9),使g(x0)=0,即2lnx0=x0-4;
故F(x)在(2,x0)上是减函数,在(x0,+∞)上是增函数;
故Fmin(x)=F(x0)=$\frac{{x}_{0}{+x}_{0}•\frac{{x}_{0}-4}{2}}{{x}_{0}-2}$=$\frac{{x}_{0}}{2}$;
故k<$\frac{{x}_{0}}{2}$;
故k的最大值是4;
故选:D.
点评 本题考查了导数的综合应用及函数零点判定定理的应用,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
10.设双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为e,则斜率为k的直线与双曲线C的左、右两支都相交的充要条件是( )
| A. | k2-e2>1 | B. | k2-e2<1 | C. | e2-k2>1 | D. | e2-k2<1 |
7.抛掷一枚质地均匀的骰子两次,记A={两次的点数均为偶数},B={两次的点数之和为8},则P(B|A)=( )
| A. | $\frac{1}{12}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
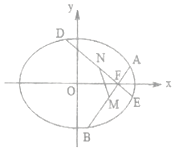 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$. 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙,刚好用两小时追赶上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙,刚好用两小时追赶上.