题目内容
9. 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙,刚好用两小时追赶上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙,刚好用两小时追赶上.(1)求渔船甲的速度;
(2)求sinC的值.
分析 (1)由题意推出∠BAC=120°,利用余弦定理求出BC=28,然后推出渔船甲的速度;
(2)在△ABC中,直接利用正弦定理求出sinC.
解答 解:(1)依题意,∠BAC=120°,AB=12海里,AC=20海里.
在ABC中,由余弦定理得,得BC2=AB2+AC2-2AB×AC×cos∠BAC.
=122+202-2×12×20×cos120°=784.
解得BC=28海里,所以渔船甲的速度是=14(海里/小时)
(2)在三角形ABC中,因为AB=12海里,∠BAC=120°,BC=28海里,
由正弦定理,得sinC=$\frac{ABsin120°}{BC}$=$\frac{3\sqrt{3}}{14}$.
点评 本题是中档题,考查三角函数在实际问题中的应用,正弦定理、余弦定理的应用,考查计算能力.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
19.已知向量$\overrightarrow a=({-2,2})$,$\overrightarrow b=({5,m})$,且|$\overrightarrow a+\overrightarrow b|$不超过5,则函数f(x)=$\sqrt{3}$cosx-sinx+m有零点的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
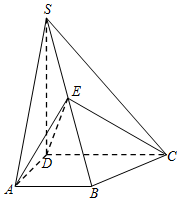 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.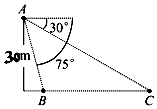 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.