题目内容
14.已知曲线$y=f(x)=\frac{4}{x}$(1)求曲线y=f(x)在点A(2,2)处的切线方程;
(2)求与曲线y=f(x)相切且过B(2,0)的直线方程.
分析 (1)求出f(x)的导数,可得切线的斜率,由点斜式方程即可得到所求切线的方程;
(2)设切点(m,$\frac{4}{m}$),求得切线的斜率和方程,代入(2,0),解方程可得m,即可得到所求切线的方程.
解答 解:(1)f(x)=$\frac{4}{x}$的导数为f′(x)=-$\frac{4}{{x}^{2}}$,
可得切线的斜率为k=-1,
切线的方程为y-2=-(x-2),
即为x+y-4=0;
(2)设切点(m,$\frac{4}{m}$),
可得切线的方程为y-$\frac{4}{m}$=-$\frac{4}{{m}^{2}}$(x-m),
即为y=-$\frac{4}{{m}^{2}}$x+$\frac{8}{m}$,
代入(2,0),可得0=-$\frac{4}{{m}^{2}}$•2+$\frac{8}{m}$,
解得m=1(0舍去),
可得过B(2,0)的直线方程为y-0=-4(x-2),
即有4x+y-8=0.
点评 本题考查导数的运用:求切线方程,考查导数的几何意义,注意区分在某点处和过某点的切线,考查方程思想,运算化简能力,属于中档题.

练习册系列答案
相关题目
4.某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,依此类推,统计结果如表:
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为a小时,求a的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠a小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
| 停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠a小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
5.cos2017°=( )
| A. | -cos37° | B. | cos37° | C. | -cos53° | D. | cos53° |
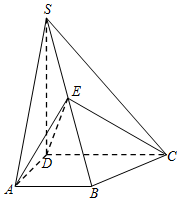 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.