题目内容
3．在焦距为2c的椭圆$M：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$中，F1，F2是椭圆的两个焦点，则“b＜c”是“椭圆M上至少存在一点P，使得PF1⊥PF2”的（ ）| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 求出椭圆M上至少存在一点P，使得PF1⊥PF2的等价条件，结合充分条件和必要条件的定义进行判断即可．
解答 解：若椭圆M上至少存在一点P，使得PF1⊥PF2，
则椭圆与半径R=c的圆满足条件．R≥b，
即b≤c，
则b＜c”是“椭圆M上至少存在一点P，
使得PF1⊥PF2”的充分不必要条件，
故选：A
点评 本题主要考查充分条件和必要条件的判断，利用椭圆的性质是解决本题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
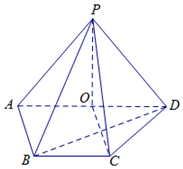如图，在四棱锥P-ABCD中，O∈AD，AD∥BC，AB⊥AD，AO=AB=BC=1，PO=$\sqrt{2}$，$PC=\sqrt{3}$．
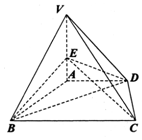如图，四棱锥V-ABCD的底面是直角梯形，VA⊥面ABCD，AD∥BC，AD⊥CD，VA=AD=CD=$\frac{1}{2}$BC=a，点E是棱VA上不同于A，V的点．
18．已知全集U=R，集合A={x|x2＞1}，那么∁UA=（ ）
| A． | [-1，1] | B． | [1，+∞） | C． | （-∞，1] | D． | （-∞，-1]∪[1，+∞） |
15．设全集U={1，2，3，4，5，6}，A={3，4}，B={2，4，5}，则（∁UA）∩B=（ ）
| A． | {1，2，4，5，6} | B． | {2，3，4，5} | C． | {2，5} | D． | {1，6} |
12．复数i（2-i）在复平面内对应的点的坐标为（ ）
| A． | （-2，1） | B． | （2，-1） | C． | （1，2） | D． | （-1，2） |