题目内容
2.已知函数f(x)=sin2x+2cos2x-1.(Ⅰ)求f(x)最小正周期;
(Ⅱ)求f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 利用三角恒等变换化简函数f(x),
即可求出(Ⅰ)函数f(x)的最小正周期,
(Ⅱ)根据x的取值范围,计算f(x)的最值.
解答 解:函数f(x)=sin2x+2cos2x-1
=sin2x+cos2x
=$\sqrt{2}sin(2x+\frac{π}{4})$;…(4分)
(Ⅰ)函数f(x)的最小正周期为:
$T=\frac{2π}{2}=π$;…(6分)
(Ⅱ)∵$x∈[0,\frac{π}{2}]$,
∴$2x+\frac{π}{4}∈[\frac{π}{4},\frac{5π}{4}]$;…(7分)
∴$sin(2x+\frac{π}{4})∈[-\frac{{\sqrt{2}}}{2},1]$;…(9分)
∴当$2x+\frac{π}{4}=\frac{5π}{4}$,即$x=\frac{π}{2}$时,f(x)取得最小值-1;…(11分)
∴当$2x+\frac{π}{4}=\frac{π}{2}$,即$x=\frac{π}{8}$时,f(x)取得最大值$\sqrt{2}$.…(13分)
点评 本题考查了三角函数的化简以及三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
12.直三棱柱A1B1C1-ABC,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{30}}}{10}$ | C. | $\frac{{\sqrt{30}}}{15}$ | D. | $\frac{{\sqrt{15}}}{10}$ |
12.复数i(2-i)在复平面内对应的点的坐标为( )
| A. | (-2,1) | B. | (2,-1) | C. | (1,2) | D. | (-1,2) |
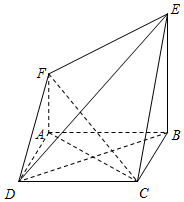 如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.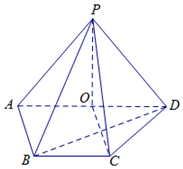 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.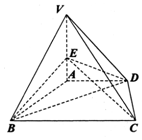 如图,四棱锥V-ABCD的底面是直角梯形,VA⊥面ABCD,AD∥BC,AD⊥CD,VA=AD=CD=$\frac{1}{2}$BC=a,点E是棱VA上不同于A,V的点.
如图,四棱锥V-ABCD的底面是直角梯形,VA⊥面ABCD,AD∥BC,AD⊥CD,VA=AD=CD=$\frac{1}{2}$BC=a,点E是棱VA上不同于A,V的点.