题目内容
1.如果平面向量$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(1,1),那么下列结论中正确的是( )| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{2}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
分析 在A中,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$;在B中,$\overrightarrow{a}•\overrightarrow{b}$=2;在C中,($\overrightarrow{a}-\overrightarrow{b}$)•$\overrightarrow{b}$=0,从而($\overrightarrow{a}-\overrightarrow{b}$)⊥$\overrightarrow{b}$;在D中,$\frac{2}{1}≠\frac{0}{1}$,从而$\overrightarrow{a}$与$\overrightarrow{b}$不平行.
解答 解:由平面向量$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(1,1),知:
在A中,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$,∴|$\overrightarrow{a}$|≠$|\overrightarrow{b}|$,故A错误;
在B中,$\overrightarrow{a}•\overrightarrow{b}$=2,故B错误;
在C中,∵$\overrightarrow{a}-\overrightarrow{b}$=(1,-1),∴($\overrightarrow{a}-\overrightarrow{b}$)•$\overrightarrow{b}$=0,∴($\overrightarrow{a}-\overrightarrow{b}$)⊥$\overrightarrow{b}$,故C正确;
在D中,∵$\frac{2}{1}≠\frac{0}{1}$,∴$\overrightarrow{a}$与$\overrightarrow{b}$不平行,故D错误.
故选:C.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意向量坐标运算法则的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $8\sqrt{3}$ | D. | $16\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 36种 | B. | 72种 | C. | 144种 | D. | 288种 |
| A. | (0,-1) | B. | (0,1) | C. | (-1,1) | D. | (1,1) |
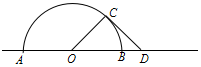 某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.
某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.