题目内容
16.已知数列{an}满足首项a1=2,an=2an-1+2n(n≥2).(Ⅰ)证明:{$\frac{{a}_{n}}{{2}^{n}}$}为等差数列并求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=log${\;}_{\sqrt{2}}$$\frac{{a}_{n}}{n}$,记数列{$\frac{1}{{b}_{n}•{b}_{n+1}}$}的前n项和为Tn,设角B是△ABC的内角,若sinBcosB>Tn,对于任意n∈N+恒成立,求角B的取值范围.
分析 (Ⅰ)根据数列的递推关系,即可得到结论.
(Ⅱ)通过(Ⅰ)计算可bn=log${\;}_{\sqrt{2}}$$\frac{{a}_{n}}{n}$=2n,进而利用裂项相消求和法计算可知Tn,利用Tn<$\frac{1}{4}$及二倍角公式化简可知$\frac{1}{2}$sin2B>Tn,结合B∈(0,π)计算即得结论.
解答 解:(Ⅰ)∵an=2an-1+2n,两边同时除以2n,可得$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+1
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=1,
又$\frac{{a}_{1}}{{2}^{1}}$=1,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是以1为首项,以1为公差的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=1+(n-1)×1=n,
∴an=n•2n;
(Ⅱ)由(Ⅰ)知,an=n•2n,则bn=log${\;}_{\sqrt{2}}$$\frac{{a}_{n}}{n}$=2n,
∴$\frac{1}{{b}_{n}•{b}_{n+1}}$=$\frac{1}{2n•2(n+1)}$=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=$\frac{1}{4}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…$\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{1}{4}$(1-$\frac{1}{n+1}$)<$\frac{1}{4}$.
又∵sinBcosB=$\frac{1}{2}$sin2B>Tn,对于任意n∈N+恒成立,
∴$\frac{1}{2}$sin2B≥$\frac{1}{4}$,即sin2B≥$\frac{1}{2}$.
又B∈(0,π),即2B∈(0,2π),
∴$\frac{π}{6}$≤2B≤$\frac{5π}{6}$,
∴B∈[$\frac{π}{12}$,$\frac{5π}{12}$].
点评 本题考查数列的通项及前n项和,考查裂项相消求和法,涉及三角函数等基础知识,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 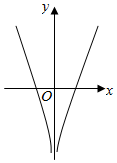 | B. | 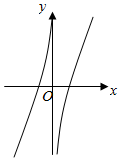 | C. | 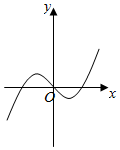 | D. |  |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{2}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
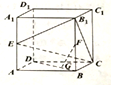 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.