题目内容
12．已知A（-3，0），B（0，4），点P为直线y=x上一点，过A，B，P三点的圆记作圆C，则“点P为原点”是“圆C的半径取得最小值”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 结合直线和圆的位置关系以及充分条件和必要条件的定义进行判断即可．
解答 解：当点P为原点时，三角形AOB是直角三角形，此时AB是圆的直径，此时圆C的半径最小，即充分性成立，
当C的半径取得最小值，AB是圆的直径，当以AB为直径的圆和直线y=x相切时，切点不是O，即必要性不成立，
则点P为原点”是“圆C的半径取得最小值”的充分不必要条件，
故选：A
点评 本题主要考查充分条件和必要条件的判断，结合直线和圆的位置关系是解决本题的关键．
练习册系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
2．已知全集U={1，2，3，4，5，6，7}，集合A={1，3，5，6，7}，B={1，2，3，4，6，7}，则A∩∁UB=（ ）
| A． | {3，6} | B． | {5} | C． | {2，4} | D． | {2，5} |
3．已知x∈R，用[x]表示不超过x的最大整数，记{x}=x-[x]，若a∈（0，1），且$\{a\}＞\{a+\frac{1}{3}\}$，则实数a的取值范围是[$\frac{2}{3}$，+∞）．
7．函数y=x2+ln|x|的图象大致为（ ）
| A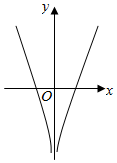． |  | B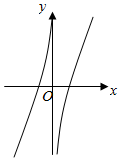． |  | C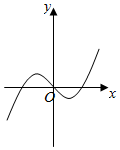． |  | D． |  |
4．已知三条不同的直线a，b，c，若a⊥b，则“a⊥c”是“b∥c”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
1．如果平面向量$\overrightarrow{a}$=（2，0），$\overrightarrow{b}$=（1，1），那么下列结论中正确的是（ ）
| A． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B． | $\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{2}$ | C． | （$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{b}$ | D． | $\overrightarrow{a}$∥$\overrightarrow{b}$ |