题目内容
11.若正三棱柱的所有棱长均为4,则其体积为( )| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $8\sqrt{3}$ | D. | $16\sqrt{3}$ |
分析 由正三棱柱ABC-A1B1C1中,所有棱长均为4,知S△ABC=$\frac{1}{2}×4×4×sin60°$=4$\sqrt{3}$,由此能求出正三棱柱ABC-A1B1C1的体积.
解答 解:如图, 正三棱柱ABC-A1B1C1中,所有棱长均为4,
正三棱柱ABC-A1B1C1中,所有棱长均为4,
∴S△ABC=$\frac{1}{2}×4×4×sin60°$=4$\sqrt{3}$,
∴正三棱柱ABC-A1B1C1的体积:
V=S△ABC×AA1=4$\sqrt{3}×4$=16$\sqrt{3}$.
故选:D.
点评 本题考查正三棱柱的体积的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )
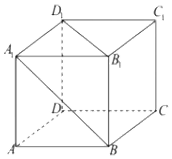

| A. | A1B∥D1B | B. | AC1⊥B1C | ||
| C. | A1B与平面DBD1B1成角为45° | D. | A1B,B1C成角为30° |
2.已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6,7},B={1,2,3,4,6,7},则A∩∁UB=( )
| A. | {3,6} | B. | {5} | C. | {2,4} | D. | {2,5} |
19.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{6}}}{2}$,则它的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{1}{4}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{\sqrt{2}}}{2}$x |
3.已知x∈R,用[x]表示不超过x的最大整数,记{x}=x-[x],若a∈(0,1),且$\{a\}>\{a+\frac{1}{3}\}$,则实数a的取值范围是[$\frac{2}{3}$,+∞).
1.如果平面向量$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(1,1),那么下列结论中正确的是( )
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{2}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
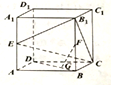 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB. 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=1,AB=2.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=1,AB=2.