题目内容
已知在△ABC中,AB=1,BC=x,AC=y,∠C=60°,求x2-y2的最大值与最小值.
考点:余弦定理,正弦定理
专题:三角函数的求值,三角函数的图像与性质
分析:由正弦定理知x=
×sinA,y=
×sin(60°+A),可得:x2-y2=-
sin(2A+60°),由0<A<120°,可得2A+60°∈(60°,300°),由正弦函数的性质即可求得x2-y2的最大值与最小值.
| 2 | ||
|
| 2 | ||
|
2
| ||
| 3 |
解答:
解:由正弦定理知,
=
=
,A+B=180°-60°=120°,
所以,x=
×sinA,y=
×sin(120°-A)=
×sin(60°+A),
即有:x2=
sin2A,y2=
sin2(60°+A),
所以可得:x2-y2=
×[sinA+sin(60°+A)][sinA-sin(60°+A)]
=
×[2sin(a+30°)cos(-30°)][2cos(A+30°)sin(-30°)]
=-
sin(2A+60°)
∵0<A<120°,
∴2A+60°∈(60°,300°),
∴sin(2A+60°)的最小值是-1,最大值是1,
所以X2-Y2的最大值是
,最小值是-
.
| 1 |
| sin60° |
| x |
| sinA |
| y |
| sinB |
所以,x=
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
即有:x2=
| 4 |
| 3 |
| 4 |
| 3 |
所以可得:x2-y2=
| 4 |
| 3 |
=
| 4 |
| 3 |
=-
2
| ||
| 3 |
∵0<A<120°,
∴2A+60°∈(60°,300°),
∴sin(2A+60°)的最小值是-1,最大值是1,
所以X2-Y2的最大值是
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题主要考查了正弦定理的应用,考查了正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
双曲线
-
=1的左右焦点为F1,F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中为真命题的是( )
A、若x≠0,则x+
| ||
| B、命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1且x≠-1,则x2≠1 | ||
| C、“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 | ||
| D、若命题P:?x∈R,x2-x+1<0,则¬P:?x∈R,x2-x+1>0 |
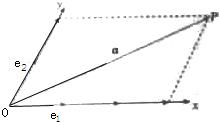 如图,设Ox、Oy是平面内相交成60°角的两条数轴,
如图,设Ox、Oy是平面内相交成60°角的两条数轴, 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6. 如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.
如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.