题目内容
已知直线y=kx+1与曲线f(x)=|x+
|-|x-
|恰有四个不同的交点,则实数k的取值范围为 .
| 1 |
| x |
| 1 |
| x |
考点:函数的图象
专题:函数的性质及应用
分析:先研究函数的奇偶性,通过分类讨论,去掉绝对值符号,画分段函数的图象,作出其图象即可得到答案.
解答:
解:函数f(x)=|x+
|-|x-
|满足f(-x)=|-x-
|-|-x+
|=|x+
|-|x-
|=f(x),故函数为偶函数,
只作出x>0时的图象即可,
当x>0时,f(x)=|x+
|-|x-
|=x+
-|x-
|=
,
则当x<0时的图象与当x>0时的图象关于y轴对称,所以函数f(x)整个函数的图象易得,在同一个坐标系画函数y=f(x)与直线y=kx+1的图象如下:
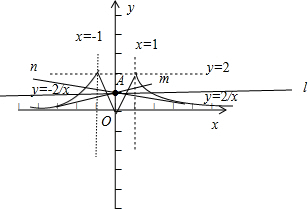
由于直线y=kx+1经过定点A(0,1),要使直线y=kx+1与曲线f(x)=|x+
|-|x-
|恰有四个不同的交点,
∴当过A点的直线m与曲线y=-
相切或直线m与曲线y=
相切时有4个交点,即有四个公共点,
设切点坐标为:(x0,y0),则k=(-
)′|x=x0=
,
∴y0=-
=kx0+1=
•x0+1,解得;x0=-4,
∴k=
;
同理,可得另一条相切时斜率为k′=-
;
当过A点的直线l∥x轴,即其斜率为0时,直线l与曲线y=f(x)|有四个公共点;
综上所述,实数k的取值范围是{
,0,-
}.
故答案为:{
,0,-
}.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
只作出x>0时的图象即可,
当x>0时,f(x)=|x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
|
则当x<0时的图象与当x>0时的图象关于y轴对称,所以函数f(x)整个函数的图象易得,在同一个坐标系画函数y=f(x)与直线y=kx+1的图象如下:

由于直线y=kx+1经过定点A(0,1),要使直线y=kx+1与曲线f(x)=|x+
| 1 |
| x |
| 1 |
| x |
∴当过A点的直线m与曲线y=-
| 2 |
| x |
| 2 |
| x |
设切点坐标为:(x0,y0),则k=(-
| 2 |
| x |
| 2 |
| x02 |
∴y0=-
| 2 |
| x0 |
| 2 |
| x02 |
∴k=
| 1 |
| 8 |
同理,可得另一条相切时斜率为k′=-
| 1 |
| 8 |
当过A点的直线l∥x轴,即其斜率为0时,直线l与曲线y=f(x)|有四个公共点;
综上所述,实数k的取值范围是{
| 1 |
| 8 |
| 1 |
| 8 |
故答案为:{
| 1 |
| 8 |
| 1 |
| 8 |
点评:本题考查带绝对值的函数,对于此类题目,去绝对值符号,把函数化为分段函数考虑是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知复数(1+i)(a+bi)=2+4i(a,b∈R),函数f(x)=2sin(ax+
)+b图象的一个对称中心是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(
|
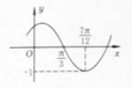 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
函数f(x)=
的图象大致是图中的( )
| cos(πx) |
| x2 |
A、 |
B、 |
C、 |
D、 |