题目内容
已知向量
=（1，3），
=（-2，m），若
⊥
，则m的值为（ ）
| a |
| b |
| a |
| b |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：直接利用向量的垂直的充要条件列出方程求解即可．
解答：
解：向量
=（1，3），
=（-2，m），
⊥
，
所以-2×1+3m=0，
解得m=
．
故选：D．
| a |
| b |
| a |
| b |
所以-2×1+3m=0，
解得m=
| 2 |
| 3 |
故选：D．
点评：本题考查向量的垂直的充要条件的应用，考查计算能力．
练习册系列答案
相关题目
如果θ角的终边经过点（-
，
），那么sin（
+θ）+cos（π-θ）+tan（2π-θ）=（ ）
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知函数y=f（x）的图象过点（2，0），那么函数y=f（x+3）-1的图象一定过下面点中的（ ）
| A、（-1，1） |
| B、（1，-1） |
| C、（-1，-1） |
| D、（1，1） |
函数y=
的定义域是（ ）
| ||
| x-2 |
A、[
| ||
B、[
| ||
C、（
| ||
| D、（-∞，2）∪（2，+∞） |
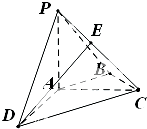如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AB=