题目内容
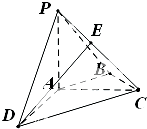 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=| 2 |
(1)求二面角A-PC-B的余弦值;
(2)设E为棱PC上的点,满足直线DE与平面PBC所成角的正弦值为
2
| ||
| 3 |
考点:直线与平面所成的角,二面角的平面角及求法
专题:空间角,空间向量及应用
分析:(1)首先建立空间直角坐标系,求出相应向量利用平面的法向量,求出向量的夹角的余弦值.
(2)同样利用法向量知识,利用夹角的正弦值作为建立等量的条件,求出点E的坐标,最后求出向量的模长.
(2)同样利用法向量知识,利用夹角的正弦值作为建立等量的条件,求出点E的坐标,最后求出向量的模长.
解答:
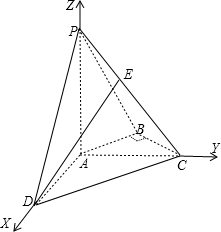
解:(1)分别以AD,AC,AP所在直线为x,y,z轴建立空间直角坐标系
平面PAC的法向量
=(1,0,0)
由已知得:P(0,0,2),C(0,2,0),B(-1,1,0)
∴
=(0,2,-2),
=(1,1,0)
设平面PBC的法向量为
=(x,y,z)
则
,即
取
=(1,-1,-1)
cos<
,
>=
=
∴二面角A-PC-B的余弦值为
(2)设E(0,1+t,1-t),则
=(-2,1+t,1-t)
由(Ⅰ)知平面PBC的法向量
=(1,-1,-1),
由于直线DE与平面PBC所成角的正弦值为
所以|cos<
,
>|=
=
=
得t=0,
=(0,1,1),
|
|=
=
,
即:AE的长等于
故答案为:(1)二面角A-PC-B的余弦值为
(2)AE的长等于

解:(1)分别以AD,AC,AP所在直线为x,y,z轴建立空间直角坐标系
平面PAC的法向量
| m |
由已知得:P(0,0,2),C(0,2,0),B(-1,1,0)
∴
| PC |
| BC |
设平面PBC的法向量为
| n |
则
|
|
取
| n |
cos<
| m |
| n |
| ||||
|
|
| ||
| 3 |
∴二面角A-PC-B的余弦值为
| ||
| 3 |
(2)设E(0,1+t,1-t),则
| DE |
由(Ⅰ)知平面PBC的法向量
| n |
由于直线DE与平面PBC所成角的正弦值为
2
| ||
| 3 |
所以|cos<
| DE |
| n |
|
| ||||
|
|
| 4 | ||||
|
2
| ||
| 3 |
得t=0,
| AE |
|
| AE |
| 02+12+12 |
| 2 |
即:AE的长等于
| 2 |
故答案为:(1)二面角A-PC-B的余弦值为
| ||
| 3 |
(2)AE的长等于
| 2 |
点评:本题考查的知识点:空间直角坐标系,平面的法向量,线面所成的角,夹角的余弦,向量的模长.

练习册系列答案
相关题目
已知向量
=(1,3),
=(-2,m),若
⊥
,则m的值为( )
| a |
| b |
| a |
| b |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
下列说法正确的是( )
A、函数y=
| ||
| B、根据函数定义,函数在不同定义域上,值域也应不同 | ||
| C、空集是任何集合的子集,但是空集没有子集 | ||
| D、函数的单调区间一定是其定义域的一个子集 |
在△ABC中,a、b,c是角A,B,C所对的边,若sinA+sin(C-B)=sin2B,且
<cosB,则△ABC的形状为( )
| c |
| a |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
y=sin(ωx+ϕ)(ω>0,|ϕ|<
)的图象的一部分图形如图所示,则函数的解析式为( )
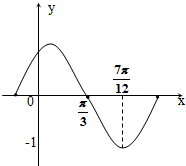
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
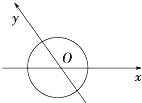 如图,Ox、Oy是平面内相交成120°的两条数轴,
如图,Ox、Oy是平面内相交成120°的两条数轴,