题目内容
函数y=
的定义域是（ ）
| ||
| x-2 |
A、[
| ||
B、[
| ||
C、（
| ||
| D、（-∞，2）∪（2，+∞） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由题意，分子根号下的式子大于或等于零，分母不为零，据此列出x的不等式组，求解即可．
解答：
解：要使原式有意义只需：
，解得x≥
且x≠2，
故函数的定义域为[
，2）∪（2，+∞）．
故答案为B．
|
| 3 |
| 2 |
故函数的定义域为[
| 3 |
| 2 |
故答案为B．
点评：求函数的定义域分两类，一是实际问题中函数的定义域，有变量的实际意义确定；二是一般函数的定义域，由使式子有意的x的范围确定，一般是列出不等式组求解．注意结果要写成集合或区间的形式．
练习册系列答案
相关题目
已知向量
=（1，3），
=（-2，m），若
⊥
，则m的值为（ ）
| a |
| b |
| a |
| b |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
定积分
dx的值是（ ）
| ∫ | 2 1 |
| 1+x2 |
| x |
A、
| ||
B、
| ||
| C、3+ln2 | ||
D、
|
定义域为R的函数y=f（x），若对任意两个不相等的实数x1，x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1），则称函数为“H函数”，现给出如下函数：
①y=-x3+x+1②y=3x-2（sinx-cosx）③y=ex+1④f(x)=
其中为“H函数”的有（ ）
①y=-x3+x+1②y=3x-2（sinx-cosx）③y=ex+1④f(x)=
|
其中为“H函数”的有（ ）
| A、①② | B、③④ | C、②③ | D、①②③ |
下列说法正确的是（ ）
A、函数y=
| ||
| B、根据函数定义，函数在不同定义域上，值域也应不同 | ||
| C、空集是任何集合的子集，但是空集没有子集 | ||
| D、函数的单调区间一定是其定义域的一个子集 |
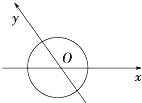如图，Ox、Oy是平面内相交成120°的两条数轴，