题目内容

8．二项式${（2x-\frac{a}{{\sqrt{x}}}）^n}$的展开式中所有项二项式系数和为64，则展开式中的常数项为60，则a的值为（　　）
A．2B．±1C．-1D．1

分析 根据二项式定理列方程求出n，再计算常数项得出a．

解答 解：∵展开式的二项式系数和为64，
∴2n=64，即n=6，
∴展开式的常数项为${C}_{6}^{4}$（2x）2（-$\frac{a}{\sqrt{x}}$）4=15×4×a4=60，
∴a=±1．
故选B．

点评 本题考查了二项式定理，属于基础题．

练习册系列答案
相关题目
18．某四面体的三视图如图所示，则其四个面中最大面的面积是（　　）
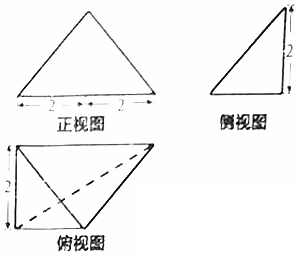
A．4B．$2\sqrt{2}$C．$2\sqrt{6}$D．$4\sqrt{2}$
19．若曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=1+2sinθ\end{array}\right.$（参数$θ∈[{-\frac{π}{2}，\frac{π}{2}}]$），则曲线C（　　）
A．表示直线B．表示线段C．表示圆D．表示半个圆
16．直角坐标系xOy中，曲线C：x2+（y-1）2=4与y轴负半轴交于点K，直线l与C相切于K，T为C上任意一点，T′为T在l上的射影，P为T，T'的中点．
（Ⅰ）求动点P的轨迹Γ的方程；
（Ⅱ）轨迹Γ与x轴交于A，B，点M，N为曲线Γ上的点，且OM∥AP，ON∥BP，试探究三角形OMN的面积是否为定值，若为定值，求出该值；若非定值，求其取值范围．
3．（$\sqrt{x}$-$\frac{1}{x}$）9展开式中的常数项是（　　）
A．-84B．84C．-36D．36
13．下列积分的值等于1的是（　　）
A．$\int_0^1{xdx}$B．${∫}_{0}^{1}$（x+1）dxC．${∫}_{0}^{1}$1dxD．${∫}_{0}^{1}$$\frac{1}{2}$dx
20．在直角坐标系中xOy，直线C1的参数方程为$\left\{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}\right.$（t是参数）．在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρ=sinθ-cosθ（θ是参数）．
（Ⅰ）将曲线C2的极坐标方程化为直角坐标方程，并判断曲线C2所表示的曲线；
（Ⅱ）若M为曲线C2上的一个动点，求点M到直线C1的距离的最大值和最小值．
17．已知函数 f（x）=|2x+1-|2x-t|（t∈R）．
　　（Ⅰ）当 t=3时，解关于x 的不等式 f（x）＜1；
　　（Ⅱ）?x∈R使得，求 f（x）≤-5，求t的取值范围．
18．如图是把二进制数11111（2）化为十进制数的一个程序框图，则输出的S=（　　）
 
A．15B．30C．31D．63

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网