题目内容
18.某四面体的三视图如图所示,则其四个面中最大面的面积是( )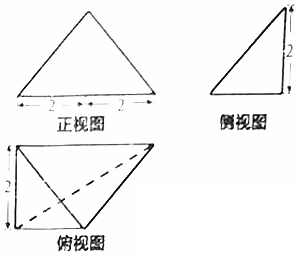
| A. | 4 | B. | $2\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $4\sqrt{2}$ |
分析 由三视图可知:该几何体为三棱锥PABC,AC⊥CB.过点P作PO⊥底面ABC,垂足为O.连接OA,则OA∥BC,OA=$\frac{1}{2}$BC.
解答 解:由三视图可知:该几何体为三棱锥PABC,AC⊥CB.过点P作PO⊥底面ABC,垂足为O.
连接OA,则OA∥BC,OA=$\frac{1}{2}$BC.
∴最大面积为△PBC,其面积S=$\frac{1}{2}×4×\sqrt{{2}^{2}+{2}^{2}}$=$4\sqrt{2}$.
故选:D.
点评 本题考查了三棱锥的三视图、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$上有不共线三点A,B,C,且AB,BC,AC的中点分别为D,E,F,若满足OD,OE,OF的斜率之和为-1,则$\frac{1}{{{k_{AB}}}}+\frac{1}{{{k_{BC}}}}+\frac{1}{{{k_{AC}}}}$=( )
| A. | 2 | B. | $-\sqrt{3}$ | C. | -2 | D. | 3 |
6.在二项式(x+$\frac{1}{2•\root{3}{x}}$)n的展开式中,若前三项系数成等差数列,则展开式中的常数项为( )
| A. | $\frac{7}{16}$ | B. | 7 | C. | 16 | D. | 28 |
10.已知四棱锥的三视图如图所示,则该四棱锥的全面积为( )
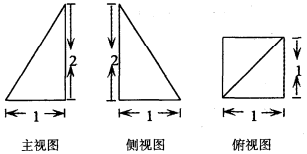

| A. | 4 | B. | 5 | C. | $2+\sqrt{5}$ | D. | $3+\sqrt{5}$ |
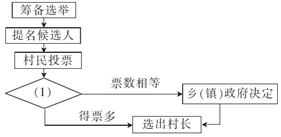 选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.
选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.