题目内容
20.在直角坐标系中xOy,直线C1的参数方程为$\left\{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}\right.$(t是参数).在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρ=sinθ-cosθ(θ是参数).(Ⅰ)将曲线C2的极坐标方程化为直角坐标方程,并判断曲线C2所表示的曲线;
(Ⅱ)若M为曲线C2上的一个动点,求点M到直线C1的距离的最大值和最小值.
分析 (I)曲线C2的极坐标方程为ρ=sinθ-cosθ(θ是参数).可得ρ2=ρ(sinθ-cosθ),利用互化公式可得直角坐标方程:通过配方可得曲线C2所表示的曲线为圆.
(Ⅱ)直线C1的参数方程为$\left\{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}\right.$(t是参数).消去参数t化为普通方程:2x-y-1=0.求出圆心C2到直线C1的距离d.可得点M到直线C1的距离的最大值为d+r,最小值为d-r.
解答 解:(I)曲线C2的极坐标方程为ρ=sinθ-cosθ(θ是参数).可得ρ2=ρ(sinθ-cosθ),化为直角坐标方程:x2+y2=y-x.
配方为:$(x+\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}$=$\frac{1}{2}$.可得曲线C2所表示的曲线为圆:圆心为C2$(-\frac{1}{2},\frac{1}{2})$,半径r=$\frac{\sqrt{2}}{2}$.
(Ⅱ)直线C1的参数方程为$\left\{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}\right.$(t是参数),消去参数t化为普通方程:2x-y-1=0.
圆心C2到直线C1的距离d=$\frac{|-\frac{1}{2}×2-\frac{1}{2}-1|}{\sqrt{5}}$=$\frac{\sqrt{5}}{2}$.
∴点M到直线C1的距离的最大值为$\frac{\sqrt{5}}{2}$+$\frac{\sqrt{2}}{2}$,最小值为$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{2}}{2}$.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案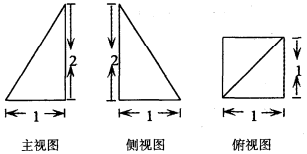
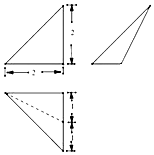
| A. | 4 | B. | 5 | C. | $2+\sqrt{5}$ | D. | $3+\sqrt{5}$ |
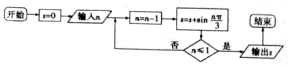
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关;
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
参考公式:${k^2}=\frac{{n(ad-bc{)^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
| A. | (0,1) | B. | (-∞,1) | C. | (0,+∞) | D. | $(-∞,\frac{1}{2})$ |
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |